Задача (4.1) называется задачей условной оптимизации (условной задачей), если Х − собственное подмножество пространства 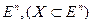 .
.
Рассмотрим конечномерную задачу условной минимизации с ограничениями типа равенств и неравенств:
f (x) 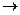 inf,
inf,
gj (x) = 0, j = 1,2..., k,
gi (x) 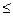 0, i = 1,2,..., m,
0, i = 1,2,..., m,
x 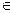 En.
En.
Предположим, что задача является гладкой, т.е. функции f (x), gj (x), j = 1,2..., k, gi (x), i = 1,2,..., m – непрерывно-дифференцируемы по х.
Допустимое множество этой задачи имеет вид
X = 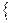 x
x 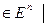 gj (x) = 0, j = 1,2..., k, gi (x) < 0, i = 1,2,..., m
gj (x) = 0, j = 1,2..., k, gi (x) < 0, i = 1,2,..., m 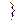 .
.
Для такой задачи сохраняют силу утверждения теорем 4.1…4.3,если её локальное решение х * является внутренней точкой допустимого множества Х (х *Îint X). Для многих условных задач минимум достигается на границе, в силу чего для них классические результаты анализа неприемлемы. Необходимо отметить, что при переходе от безусловных задач к условным все вопросы оптимизации становятся более сложными.
В дальнейшем мы часто будем прибегать к геометрической интерпретации задач оптимизации, где 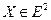 , основанной на понятии линий (или поверхностей) уровня функции ¦(x). Линией уровня функции f (x) называют геометрическое место точек, в которых функция f( x ) принимает одно и тоже значение, т.е. множества вида
, основанной на понятии линий (или поверхностей) уровня функции ¦(x). Линией уровня функции f (x) называют геометрическое место точек, в которых функция f( x ) принимает одно и тоже значение, т.е. множества вида
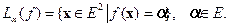
Для геометрической интерпретации данной двумерной задачи необходимо изобразить её допустимое множество Х и несколько характерных линий уровня целевой фунции ¦ (х) (рис.4.9).
Чтобы отразить характер изменения функции, у данной линии уровня  полезно ставить знак “+ “ с той стороны, где ¦ принимает значения большие a, и знак “ - “ с другой.
полезно ставить знак “+ “ с той стороны, где ¦ принимает значения большие a, и знак “ - “ с другой.
В оптимизационных задачах особое значение имеет направление наискорейшего возрастания (убывания) целевой функции, определяемое градиентом (антиградиентом) этой функции (см. п.3.2.3.).
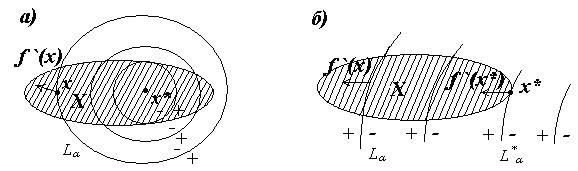
Рис. 4.9. Геометрическая интерпритация задача оптимизации
Градиент функции ¦(x,y) в каждой точке  (x, y) направлен по нормали к линии уровня поверхности
(x, y) направлен по нормали к линии уровня поверхности 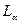 , проходящей через эту точку. Понятие градиента легко обобщается на случай функции n переменных.
, проходящей через эту точку. Понятие градиента легко обобщается на случай функции n переменных.
Если функция 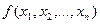 дифференцируема в точке
дифференцируема в точке 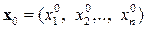 , то градиентом Ѧ(x) в точке
, то градиентом Ѧ(x) в точке 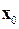 называется n -мерный вектор, координаты которого равны частным производным функции ¦(х), вычисленным в точке
называется n -мерный вектор, координаты которого равны частным производным функции ¦(х), вычисленным в точке 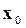 , т.е.
, т.е.
Ѧ(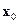 )=
)= 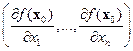 .
.
Если функция ¦ дифференцируема в точке х, то градиент Ѧ(x) ортогонален к проходящей через х линии уровня и направлен (если естественно Ѧ(x) ¹ 0) в сторону возрастания функции, т.е. в сторону знака “+”. В геометрическом плане поиск глобального решения сводится к нахождению минимального числа a* среди всех a таких, что линия уровня L a имеет непустое пересечение с Х. При этом любая точка х *Î 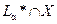 является глобальным решением задачи, а сама
является глобальным решением задачи, а сама 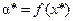 – минимальным значением функции ¦ на Х. Возможны два случая: х * лежит внутри (рис. 4.9,а) и на границе (рис. 4.9,б) множества Х.
– минимальным значением функции ¦ на Х. Возможны два случая: х * лежит внутри (рис. 4.9,а) и на границе (рис. 4.9,б) множества Х.
Однако только геометрический метод решения никак не может удовлетворить инженеров. Возможны «технические» погрешности, которые неизбежно возникают при приближённом построении графиков. Кроме того, его можно применить только в том случае, когда число переменных в стандартной задаче равно двум. Поэтому необходимы аналитические методы, позволяющие решать задачи с любым числом переменных и выявлять физический, технический, экономический смысл входящих в них величин. Эти методы будут рассмотрены в следующих главах.
 2015-02-04
2015-02-04 1224
1224