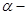Такой тип умножения возникает при перемножении двух векторов, когда в результате должен получиться скаляр. Примером является вычисление работы некоторой силы над некоторым движущимся телом
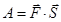 .
.
Если векторы 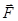 и
и 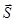 заданы координатами, то их скалярное произведение
заданы координатами, то их скалярное произведение 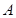 может быть определено с помощью формулы
может быть определено с помощью формулы
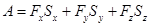 .
.
Если же известны модули перемножаемых векторов и угол между ними, то
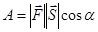 ,
,
Если некоторый вектор 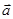 составляет угол
составляет угол 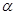 с осью ОХ, то проекция вектора
с осью ОХ, то проекция вектора 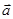 на эту ось равна
на эту ось равна
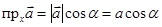 .
.
Это же выражение справедливо и для других осей координат, а также и для некоторой прямой, положение которой в пространстве или на плоскости известно.
Проекция суммы векторов на некоторую ось равна сумме проекций векторов на эту ось
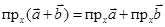 .
.
В соответствии с (1.5.6.) угол 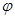 между векторами
между векторами 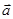 и
и 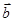
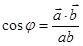 .
.
Свойства скалярного произведения векторов:
- 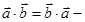 переместительный закон (коммутативность скалярного произведения);
переместительный закон (коммутативность скалярного произведения);
- 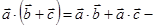 распределительный закон (дистрибутивность скалярного произведения);
распределительный закон (дистрибутивность скалярного произведения);
- если 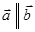 , то
, то 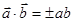 , скалярный квадрат некоторого вектора
, скалярный квадрат некоторого вектора 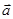
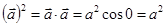 , очевидно, что
, очевидно, что 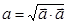
|
|
|
- если 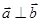 , то
, то 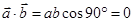 .
.
 2015-02-27
2015-02-27 725
725