2015-02-27
1475
Определение. Базисом системы векторов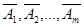 
называется совокупность линейно независимых векторов данной системы, число которых равно ее рангу.
Определение. Любая система n линейно независимых векторов n-мерного векторного пространства называется базисом этого пространства.
Определение. Линейно независимые векторы 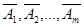образуют базис рассматриваемого векторного пространства, если любой вектор 
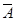этого пространства является линейной комбинацией этих векторов, т.е.
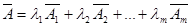, где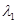 
- некоторые числа.
В этом случае говорят, что вектор 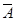разложен по данному базису, а числа 
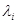называют координатами вектора 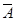по данному базису. При изменении базиса координаты вектора могут измениться.
Теорема: Каждый вектор линейного пространства можно представить, и притом единственным образом, в виде линейной комбинации векторов базиса.
Пусть векторы 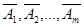образуют базис. Возьмем произвольный вектор 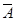. Вектор 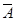можно представить в виде линейной комбинации базисных векторов .
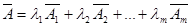Это равенство называют разложением вектора 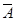по базису 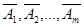, а числа 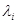называют координатами вектора 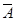по данному базису. При изменении базиса координаты вектора могут измениться.
