Средняя арифметическая скорость

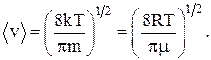
Относительная скорость применяется для расчета числа молекул, движущихся со скоростями в интервале от v до v + dv:

u = v/v_в.

Закон распределения молекул идеального газа по скоростям в стационарном состоянии (распределение Максвелла):

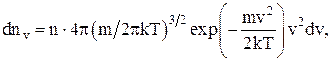
где dn_v – среднее число молекул в единице объема со скоростями в интервале от v до v + dv;

n – число молекул в единице объема.

Функция распределения (доля молекул от их общего числа отнесена к некоторому интервалу скоростей):

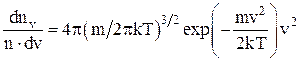
или

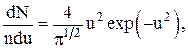
где dn_v/ndv – функция распределения.

Свободные пробеги молекул – прямолинейные участки траектории, проходимые молекулой между двумя последовательными соударениями.

Средняя длина свободного пробега молекулы – среднее расстояние, проходимое молекулой между двумя соударениями:

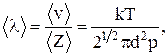
где Z – число соударений;

<v> – средняя скорость молекулы;

k – постоянная Больцмана;

<d> – диаметр молекулы;

p – давление;

T – абсолютная температура.

Среднее число соударений <z> – число соударений молекул, численно равное отношению средней скорости движения молекул <v> к средней длине свободного пробега:

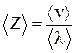, или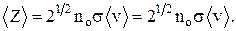

Эффективный диаметр молекулы d – минимальное расстояние, на которое сближаются при столкновении центры 2–х молекул.

Эффективное сечение – величина равная

s = pd².

Барометрическая формула показывает, что давление убывает с высотой тем быстрее, чем тяжелее газ и чем ниже его температура:

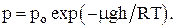
Закон распределения молекул газа по высоте в поле сил тяготения (распределение Больцмана):

, ,

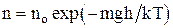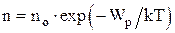где n_o – число молекул в единице объема в том месте, где потенциальная энергия молекул равна нулю;

n – число молекул в единице объема в тех точках пространства, где потенциальная энергия молекул равна W_p.

Распределение Максвелла–Больцмана – благодаря этому распределению можно определить долю молекул идеального газа, имеющих скорости в интервале от v до v + dv и обладающих потенциалом c = gh во внешнем силовом поле:

,

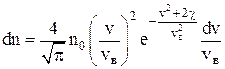где v_в – наиболее вероятная скорость, значению которой соответствует максимум кривой Максвелла.

Зависимость плотности газа от высоты:

; ,

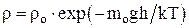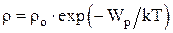где m_o – масса одной молекулы.