81 - 90. Дано комплексное число а. Требуется:1) записать число а в алгебраической и тригонометрической формах; 2) найти все корни уравнения z3 + а = 0.
81. 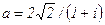 . 82.
. 82. 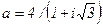 .
.
83. 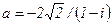 . 84.
. 84. 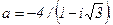
85. 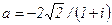 . 86.
. 86. 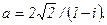
87. 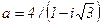 . 88.
. 88. 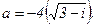 .
.
89. 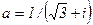 . 90.
. 90. 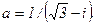 .
.
91 - 95. Построить график функции у = Аsin(ax+b) преобразованием графика функции у = sin x.
91. 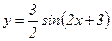 .
.
92. 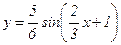 .
.
93. 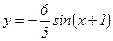 .
.
94. 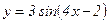 .
.
95. 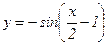 .
.
96 - 100. Построить график функции y = A cos(ax+b) преобразованием графика функции y = cos x.
96. 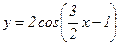 .
.
97. 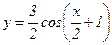 .
.
98. 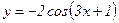 .
.
99. 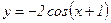 .
.
100. 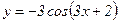 .
.
101 - 120. Найти пределы функций, не пользуясь правилом Лопиталя.
| 101. | а) 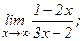 | б) 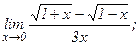 |
в) 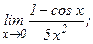 | г) 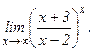 | |
| 102. | а) 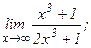 | б) 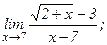 |
в) 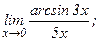 | г) 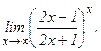 | |
| 103. | а) 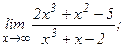 | б) 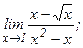 |
в) 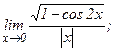 | г) 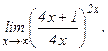 | |
| 104. | а) 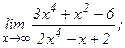 | б) 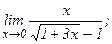 |
в) 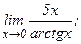 | г) 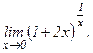 | |
| 105. | а) 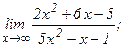 | б) 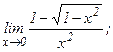 |
в) 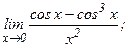 | г) 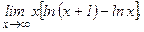 | |
| 106. | а) 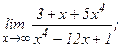 | б) 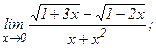 |
в) 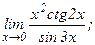 | г) 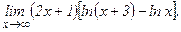 | |
| 107. | а) 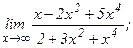 | б) 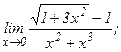 |
в) 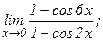 | г) 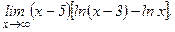 | |
| 108. | а) 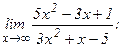 | б) 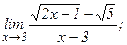 |
в) 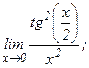 | г) 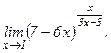 | |
| 109. | а) 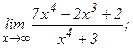 | б) 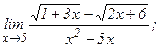 |
в) 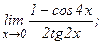 | г) 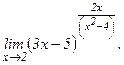 | |
| 110. | а) 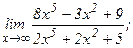 | б) 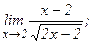 |
в) 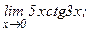 | г) 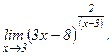 | |
| 111. | а) 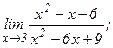 | б) 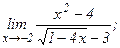 |
в) 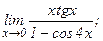 | г) 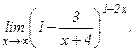 | |
| 112. | а) 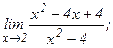 | б) 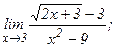 |
в) 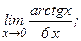 | г) 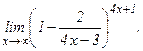 | |
| 113. | а) 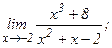 | б) 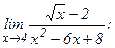 |
в) 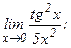 | г) 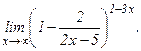 | |
| 114. | а) 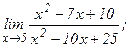 | б) 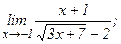 |
в) 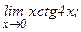 | г) 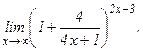 | |
| 115. | а) 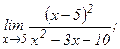 | б) 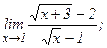 |
в) 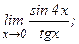 | г) 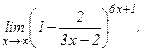 | |
| 116. | а) 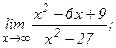 | б) 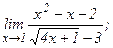 |
в) 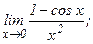 | г) 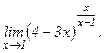 | |
| 117. | а) 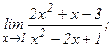 | б) 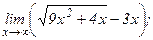 |
в) 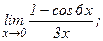 | г) 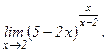 | |
| 118. | а) 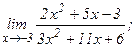 | б) 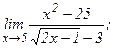 |
в) 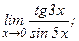 | г) 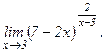 | |
| 119. | а) 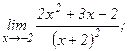 | б) 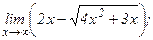 |
в) 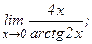 | г) 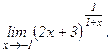 | |
| 120. | а) 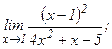 | б) 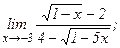 |
в) 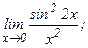 | г) 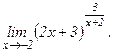 |
121 - 130. Задана функция y = f(x) и два значения аргумента х1 и х2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти ее пределы в точке разрыва слева и справа; 3) сделать схематический чертеж.
121. f(x)=91/(2-x), x1=0, x2=2.
123. f(x)=121/x, x1=0, x2=2.
125. f(x)=81/(5-x), x1=3, x2=5.
127. f(x)=141/(6-x), x1=4, x2=6.
129. f(x)=111/(4+x), x1=-4, x2=-2.
122. f(x)=41/(3-x), x1=1, x2=3.
124. f(x)=31/(4-x), x1=2, x2=4.
126. f(x)=101/(7-x), x1=5, x2=7.
128. f(x)=151/(8-x), x1=6, x2=8.
130. f(x)=131/(5+x), x1=-5, x2=-3.
В задачах 131 - 140 даны функции y = f(x) и значения аргумента х1 и х2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной при данных значениях аргумента; 2) найти односторонние пределы в точках разрыва; 3)построить график данной функции.
131. 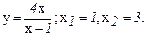
133. 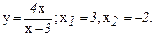
135. 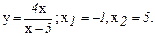
137. 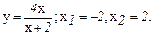
139. 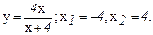
132. 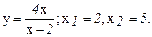
134 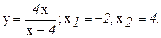
136. 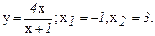
138. 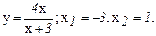
140. 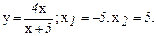
В задачах 141 - 150 функция у задана различными аналитическими выражениями для различных областей изменения аргумента х. Требуется: 1) найти точки разрыва функции, если они существуют; 2) найти односторонние пределы и скачок функции в точках разрыва; 3) сделать чертеж.
| 141. | 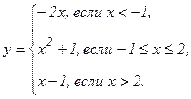 | 146. | 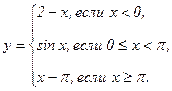 |
| 142. | 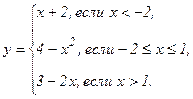 | 147. | 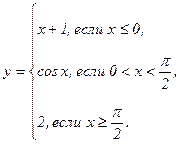 |
| 143. | 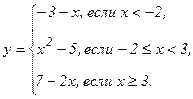 | 148. | 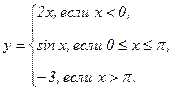 |
| 144. | 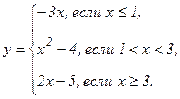 | 149. | 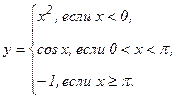 |
| 145. | 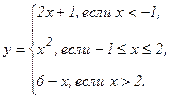 | 150. | 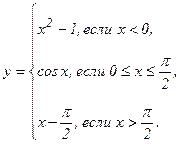 |
151 - 160. Задана функция y = f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
151. 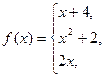
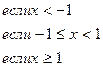
152. 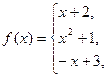
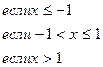
153. 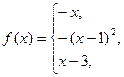
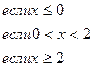
154. 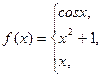
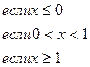
155. 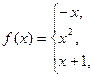
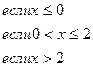
156. 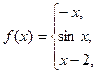
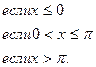
157. 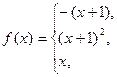
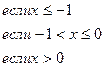
158. 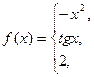
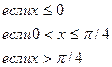
159. 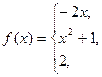
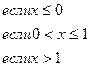
160. 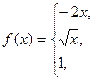
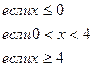
 2015-02-27
2015-02-27 935
935








