Изучение тенденции развития явлений (процессов)

Всякий ряд динамики теоретически может быть представлен в виде:

- тренда – основной тенденции развития динамического ряда (к увеличению либо снижению его уровней);

- циклических (периодических) колебаний, в том числе сезонных;

- случайных колебаний.

Изучение тренда включает два основных этапа:

1) ряд динамики проверяется на наличие тренда;

2) производится выравнивание временного ряда и непосредственное выделение тренда с экстраполяцией полученных результатов.

Непосредственное выделение тренда может быть произведено тремя методами.

1. Укрупнение интервалов. Ряд динамики разделяют на некоторое достаточно большое число равных интервалов. Если средние уровни по интервалам не позволяют увидеть тенденцию развития явления, переходят к расчету уровней за большие промежутки времени, увеличивая длину каждого интервала (одновременно уменьшается количество интервалов).

2. Скользящая средняя. В этом методе исходные уровни ряда заменяются средними величинами, которые получают из данного уровня и нескольких симметрично его окружающих. Целое число уровней, по которым рассчитывается среднее значение, называют интервалом сглаживания. Интервал может быть нечетным (3, 5, 7 и т.д. точек) или четным (2, 4, 6 и т.д. точек).

При нечетном сглаживании полученное среднее арифметическое значение закрепляют за серединой расчетного интервала, при четном этого делать нельзя. Поэтому при обработке ряда с четными интервалами их искусственно делают нечетными, для чего образуют ближайший больший нечетный интервал, но из крайних его уровней берут только 50%.

Пример. По данным (табл. 7.6) об урожайности пшеницы за 16 лет рассчитать: трех и семилетние скользящие средние:

Таблица 7.6 – Исходные данные

t
Yt	10,3	14,3	7,7	15,8	14,4	16,7	15,3	20,2
t
Yt	17,1	7,7	15,3	16,3	19,9	14,4	18,7	20,7

Решение:

Таблица 7.7 - Расчет скользящих средних

t	Yt	Простые скользящие средние	Взвешенная скользящая средняя	t	Yt	Простые скользящие средние	Взвешенная скользящая средняя
трех-летняя	семи-летняя	трех-летняя	семи-летняя
	10,3	-	-	-		17,1	15,0	16,0	15,2
	14,3	10,8	-	-		7,7	13,4	15,8	11,7
	7,7	12,6	-	11,9		15,3	13,1	15,6	12,5
	15,8	12,6	13,5	12,6		16,3	17,2	16,1	18,1
	14,4	15,6	14,9	16,2		19,9	16,9	-	17,3
	16,7	15,5	15,3	15,2		14,4	17,0	-	17,1
	15,3	17,4	15,2	17,4		18,7	17,7	-	-
	20,2	17,5	15,5	18,8		20,7	-	-	-

При трехлетней скользящей средней:

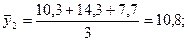
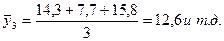
При семилетней скользящей средней:

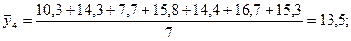
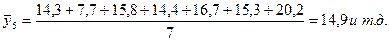
Графический анализ показывает, что ряд, сглаженный по 7-летней скользящей средней, носит более гладкий характер.

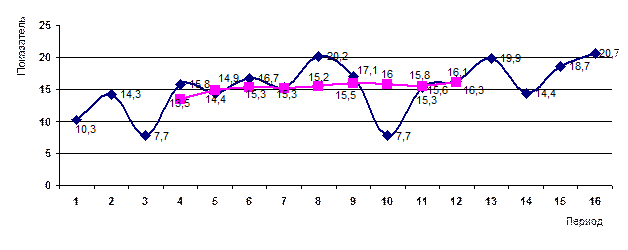
Рисунок 7.1 – Сглаживание ряда урожайности пшеницы с помощью скользящих средних

Метод простой скользящей средней применим, если напоминает прямую. Если для процесса характерно нелинейное развитие, то простая скользящая средняя может привести к существенным искажениям. В этих случаях более надежным является использование взвешенной скользящей средней. Простая скользящая средняя учитывает все уровни ряда, входящие в участок сглаживания, с равными весами, а взвешенная средняя приписывает каждому уровню вес, зависящий от удаления данного уровня от уровня, стоящего в середине участка. В таблице 7.8 представлены коэффициенты при сглаживании по полиному 2 или 3 порядка (в зависимости от длины интервала сглаживания).

Таблица 7.8 – Весовые коэффициенты при сглаживании полиномом 2-го и 3-го порядка

Длина интервала сглаживания	Весовые коэффициенты
	1/35(-3;+12;+17)
	1/21(-2;+3;+6;+7)
	1/231(-21;+14;+39;+54;+59)
	1/429(-36;+9;+44;+69;+84;+89)

Пример: Рассчитать по данным таблицы 7.6 5-летнюю взвешенную скользящую среднюю.

Решение: для вычисления значений 5-летней взвешенной скользящей воспользуемся данными таблицы 7.8:

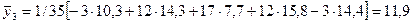
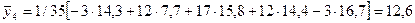и т.д. см. таб.8,5.

3. Аналитическое выравнивание. Под этим понимают определение основной проявляющейся во времени тенденции развития изучаемого явления. Развитие предстает перед исследователем как бы в зависимости только от течения времени. В итоге выравнивания временного ряда получают наиболее общий, суммарный, проявляющийся во времени результат действия всех причинных факторов. Отклонение конкретных уровней ряда от уровней, соответствующих общей тенденции, объясняют действием факторов, проявляющихся случайно или циклически. В результате приходят к трендовой модели

,

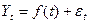где f(t)– уровень, определяемый тенденцией развития;

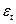– случайное и циклическое отклонение от тенденции.

Целью аналитического выравнивания динамического ряда является определение аналитической или графической зависимости f(t). На практике по имеющемуся временному ряду задают вид и находят параметры функции f(t), а затем анализируют поведение отклонений от тенденции. Функцию f(t) выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса.

Чаще всего при выравнивании используются следующие зависимости:

линейная ;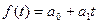

параболическая ;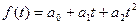

экспоненциальная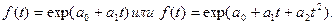

Линейная зависимость выбирается в тех случаях, когда в исходном временном ряду наблюдаются более или менее постоянные абсолютные цепные приросты, не проявляющие тенденции ни к увеличению, ни к снижению.

Параболическая зависимость используется, если абсолютные цепные приросты сами по себе обнаруживают некоторую тенденцию развития, но абсолютные цепные приросты абсолютных цепных приростов (разности второго порядка) никакой тенденции развития не проявляют.

Экспоненциальная зависимость применяются, если в исходном временном ряду наблюдается либо более или менее постоянный относительный рост (устойчивость цепных темпов роста, темпов прироста, коэффициентов роста), либо, при отсутствии такого постоянства, – устойчивость в изменении показателей относительного роста (цепных темпов роста цепных же темпов роста, цепных коэффициентов роста цепных же коэффициентов или темпов роста и т.п.).

Оценка параметров (а₀,а₁,а₂) осуществляется преимущественно методом наименьших квадратов, который обеспечивает наименьшую сумму квадратов отклонений фактических уровней от выровненных: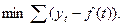

Математический аппарат метода наименьших квадратов описан в математической статистике. Так, решение системы нормальных уравнений в результате минимизации квадратов отклонений фактических уровней динамического ряда от их выровненного значения, позволяет отыскать параметры а₀,а₁,а_2.

Например, система нормальных уравнений для нахождения параметров прямой:

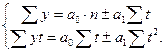(7.8)

для параболы 2-го порядка:

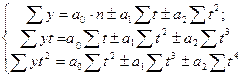(7.9)

Для упрощения расчетов допускается перенос начала координат в середину ряда динамики. Это позволяет упростить сами нормальные уравнения, а также уменьшить абсолютные значения величин, участвующих в расчете. Если до переноса начала координат t было равно 1,2,3,…, то после переноса:

- для четного числа членов ряда t =…,-5; -3; -1; 1; 3; 5;…

- для нечетного числа членов ряда t = …, -3; -2; -1; 0; 1; 2; 3; …

В этом случае оценка параметров функции имеет вид:

Для прямой: 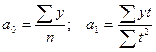. (7.10)

Пример. Имеются данные о численности населения города за пять лет на начало года. Построить модель линейного тренда и определить численность населения в 2013 году.

Таблица 7.9 – Исходные данные

Годы	Численность населения, тыс.чел., y	Номер периода t	Расчетные данные
t2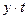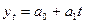
					73,0
					77,5
					82,0
					86,5
					91,0
Итого		-			410,0

Решение:

Для нахождения параметров а₀ и а₁ решаем систему уравнений, отвечающих требованиям способа наименьших квадратов:

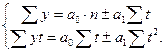
Подставляем найденные значения:

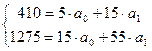
Решение системы уравнений дает следующие результаты: а₀ = 68,5 и а₁= 4,5.

Тогда 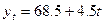. Подставляем в это уравнение значения t: 1,2,3,4,5. Находим выровненные (теоретические) значения . Длительность прогнозируемого периода не должна превышать 25% от анализируемого периода.

Вывод: а₀ = 68,5 тыс. чел. Это исходный уровень численности населения до 2008 года; а₁= 4,5 тыс. чел. – показывает, что ежегодно за период с 2008 по 2012 годы в городе происходит увеличение численности населения на 4,5 тыс. человек.