Выясним особенности расположения прямой 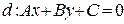 относительно аффинной системы координат
относительно аффинной системы координат 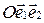 , если некоторые из чисел А, В и С равны нулю.
, если некоторые из чисел А, В и С равны нулю.
1) Пусть С =0. Тогда уравнение прямой  примет вид:
примет вид: 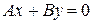 . Подставляя координаты точки
. Подставляя координаты точки 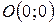 в это уравнение, убеждаемся, что получается верное равенство
в это уравнение, убеждаемся, что получается верное равенство
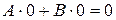 ,
,
следовательно, 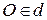 , т.е. прямая
, т.е. прямая  проходит через начало координат.
проходит через начало координат.
Обратно, пусть 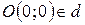 . Тогда
. Тогда 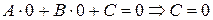 .
.
Итак, 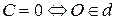 .
.
2) Пусть 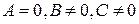 . Тогда
. Тогда 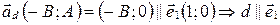 . Учитывая, что
. Учитывая, что  , получаем, что
, получаем, что 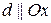 .
.
Обратно, если 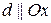 , то
, то 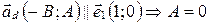 .
.
Итак, 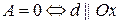 .
.
При этом уравнение  имеет вид
имеет вид 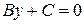 или
или  (где
(где 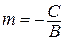 ).
).
3) Утверждение «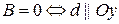 » предлагаем читателю доказать самостоятельно.
» предлагаем читателю доказать самостоятельно.
Из пунктов 1) и 2) следует пункт
4) А =0 и С =0  совпадает с осью
совпадает с осью 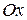 . В этом случае прямая
. В этом случае прямая  (т.е. ось
(т.е. ось 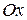 ) задается уравнением
) задается уравнением 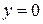 .
.
Из пунктов 1) и 3) следует пункт
5) В =0 и С =0  совпадает с осью
совпадает с осью 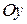 . В этом случае прямая
. В этом случае прямая  (т.е. ось
(т.е. ось 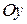 ) задается уравнением
) задается уравнением 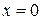 .
.
 2015-02-27
2015-02-27 346
346








