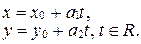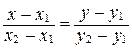Говорят, что уравнение 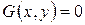 есть уравнение линии
есть уравнение линии 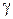 , если выполняются два условия:
, если выполняются два условия:
1) если точка 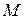 принадлежит линии
принадлежит линии 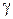 , то ее координаты удовлетворяют уравнению
, то ее координаты удовлетворяют уравнению 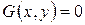 ;
;
2) если координаты точки 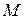 удовлетворяют уравнению
удовлетворяют уравнению 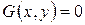 , то
, то 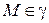 .
.
Заметим, что условие 2) можно заменить на эквивалентное ему условие 2*):
2*) если 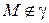 , то ее координаты не удовлетворяют уравнению
, то ее координаты не удовлетворяют уравнению 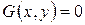 .
.
Линия на плоскости называется алгебраической, если в какой-либо аффинной системе координат уравнение этой линии можно представить в 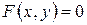 , где
, где 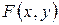 - многочлен от переменных
- многочлен от переменных 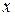 и
и 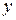 , т.е. сумма членов вида
, т.е. сумма членов вида 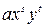 ,
, 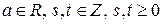 .
.
Число 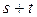 называется степенью члена
называется степенью члена 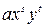 , где
, где 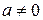 .
.
Наивысшая степень членов многочлена 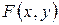 называется степенью этого многочлена. Например, степень многочлена
называется степенью этого многочлена. Например, степень многочлена 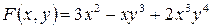 равна 7.
равна 7.
Порядком алгебраической линии, заданной уравнением 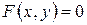 , называется степень многочлена
, называется степень многочлена 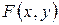 .
.
Из школьного курса известно, что прямая линия является линией первого порядка, а окружность, гипербола и парабола – линиями второго порядка.
Рассмотрим на плоскости прямую линию. Любой ненулевой вектор, параллельный данной прямой, называется ее направляющим вектором. Направляющий вектор прямой 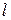 будем обозначать через
будем обозначать через 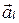 . Прямая имеет бесконечное множество направляющих векторов. Любые два из них коллинеарны (рис. 54).
. Прямая имеет бесконечное множество направляющих векторов. Любые два из них коллинеарны (рис. 54).
Прямая на плоскости однозначно задается точкой и направляющим вектором или двумя точками.
Выведем несколько уравнений прямой на плоскости в аффинной системе координат 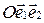 .
.
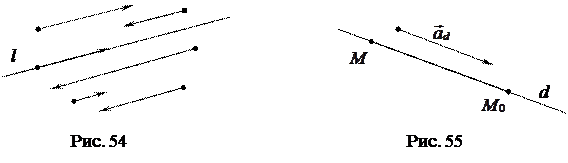 |
1. Каноническое уравнение прямой.
Пусть прямая  задана точкой
задана точкой 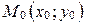 и направляющим вектором
и направляющим вектором 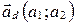 (рис. 55). Этот факт будем обозначать так:
(рис. 55). Этот факт будем обозначать так: 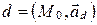 .
.
Если точка 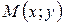 принадлежит прямой
принадлежит прямой  , то
, то 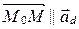 . Находим координаты вектора
. Находим координаты вектора 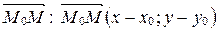 . Далее применяем условие коллинеарности двух векторов в координатах (см. § 5, свойство координат векторов 50):
. Далее применяем условие коллинеарности двух векторов в координатах (см. § 5, свойство координат векторов 50):
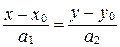 , если
, если 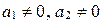 ;
;
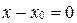 , если
, если 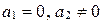 ;
;
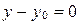 , если
, если 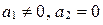 .
.
 Если
Если 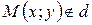 , то
, то 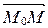 ||
|| 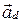 . Следовательно,
. Следовательно,
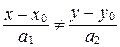 , если
, если 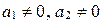 ;
;
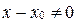 , если
, если 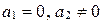 ;
;
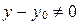 , если
, если 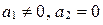 .
.
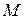 принадлежит прямой
принадлежит прямой  тогда и только тогда, когда ее координаты удовлетворяют уравнению
тогда и только тогда, когда ее координаты удовлетворяют уравнению 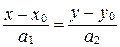 (если
(если 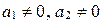 ); (10)
); (10)
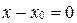 (если
(если 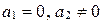 ); (11)
); (11) 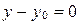 (если
(если 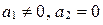 ). (12)
). (12) Каждое из уравнений (10), (11) и (12) называется каноническим уравнением прямой на плоскости.
В уравнениях (10)-(12) 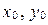 - координаты фиксированной точки
- координаты фиксированной точки 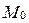 прямой
прямой  ;
; 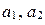 - координаты направляющего вектора прямой
- координаты направляющего вектора прямой  ;
; 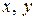 - текущие координаты произвольной точки прямой
- текущие координаты произвольной точки прямой  .
.
2. Параметрическое уравнение прямой.
Пусть прямая  задана точкой
задана точкой 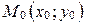 и направляющим вектором
и направляющим вектором 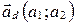 .
.
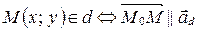 (рис. 54)
(рис. 54) 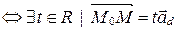 (по теореме о коллинеарных векторах).
(по теореме о коллинеарных векторах).

|

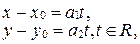 или (13)
или (13)
Система уравнений (13) называется параметрическим уравнением прямой на плоскости. Действительное число 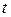 называется параметром. Геометрический смысл параметра
называется параметром. Геометрический смысл параметра 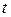 состоит в следующем: для любой точки
состоит в следующем: для любой точки 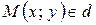 существует единственный параметр
существует единственный параметр 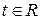 , удовлетворяющий уравнениям (13), и обратно,
, удовлетворяющий уравнениям (13), и обратно, 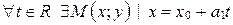 и
и 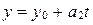 .
.
3. Уравнение прямой, заданной двумя точками.
Пусть 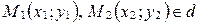 (рис. 56). Тогда в качестве направляющего вектора прямой
(рис. 56). Тогда в качестве направляющего вектора прямой  можно взять вектор
можно взять вектор 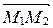 , т.е.
, т.е.
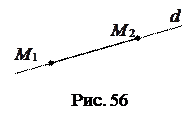
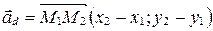 .
.
|
 задана точкой
задана точкой 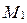 и направляющим вектором
и направляющим вектором 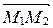 . Применяем каноническое уравнение прямой (10) (см. пункт 1):
. Применяем каноническое уравнение прямой (10) (см. пункт 1): (14)
Уравнение (14) называется уравнением прямой, заданной на плоскости двумя точками 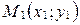 и
и 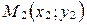 .
.
Заметим, что если 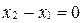 или
или 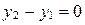 , то применяем частные случаи (11) или (12) канонического уравнения прямой.
, то применяем частные случаи (11) или (12) канонического уравнения прямой.
4. Уравнение прямой в «отрезках».
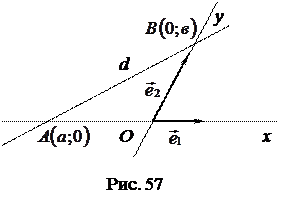 Пусть прямая
Пусть прямая  пересекает ось
пересекает ось 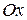 аффинной системы координат
аффинной системы координат 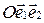 в точке
в точке 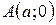 , ось
, ось 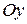 - в точке
- в точке 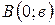 , где
, где 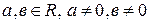 (рис. 57).
(рис. 57).
Применяя уравнение прямой, заданной двумя точками А и В, получим:
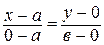 ;
;
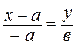 ;
; 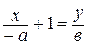 ,
,
откуда получаем уравнение:
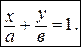 (15)
(15)
Уравнение (15) называется уравнением прямой «в отрезках».
Геометрический смысл а и в в уравнении прямой «в отрезках»: а – это абсцисса точки пересечения прямой  с осью
с осью 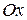 , в – ордината точки пересечения прямой
, в – ордината точки пересечения прямой  с осью
с осью 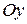 аффинной системы координат.
аффинной системы координат.
5. Уравнение прямой, заданной точкой и угловым коэффициентом.
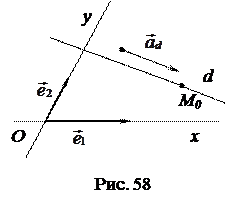 Пусть
Пусть  - прямая, не параллельная оси
- прямая, не параллельная оси 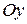 (рис. 58),
(рис. 58), 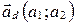 - направляющий вектор прямой
- направляющий вектор прямой  . Так как
. Так как  ||
|| 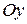 , а
, а 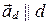 , то
, то 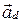 ||
|| 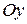 . Следовательно,
. Следовательно, 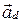 ||
|| 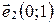 . Поэтому
. Поэтому 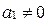 (см. условие коллинеарности векторов в координатах).
(см. условие коллинеарности векторов в координатах).
Число 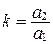 называется угловым коэффициентом прямой
называется угловым коэффициентом прямой  .
.
Угловой коэффициент прямой не зависит от выбора направляющего вектора этой прямой (попробуйте доказать это самостоятельно).
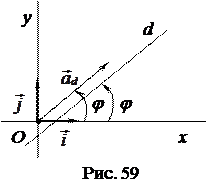 Замечание. Если прямая
Замечание. Если прямая  задана в прямоугольной системе координат
задана в прямоугольной системе координат 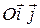 , то
, то 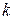 имеет простой геометрический смысл:
имеет простой геометрический смысл:  , где
, где 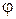 - угол наклона прямой
- угол наклона прямой  к оси
к оси 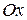 , т.е. направленный угол
, т.е. направленный угол 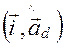 (рис. 59).
(рис. 59).
Пусть прямая  задана точкой
задана точкой 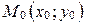 и угловым коэффициентом
и угловым коэффициентом 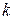 . Запишем каноническое уравнение прямой
. Запишем каноническое уравнение прямой  :
:
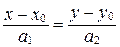
и преобразуем его: 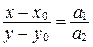 ;
; 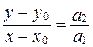 ; учитывая, что
; учитывая, что 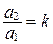 , получим:
, получим:
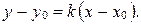 (16)
(16)
Уравнение (16) называется уравнением прямой, заданной точкой и угловым коэффициентом.
6. Уравнение прямой с угловым коэффициентом.
Пусть 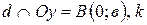 - угловой коэффициент прямой
- угловой коэффициент прямой  . Применяя уравнение (16), получим:
. Применяя уравнение (16), получим: 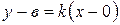 , т.е.
, т.е.
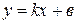 . (17)
. (17)
Уравнение (17) называется уравнением прямой с угловым коэффициентом.
В уравнении (17) в – это ордината точки пересечения прямой  с осью
с осью 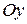 .
.
 2015-02-27
2015-02-27 1788
1788