Определение тензора второго ранга

Простейшим тензором второго ранга является диада – упорядоченная пара векторов 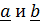, которая записывается единым символом 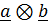(или 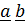); знак (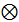) (или отсутствие знака) называется знаком тензорного умножения. Термин «упорядоченная» означает, что .

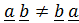Тензоры будем обозначать буквами с двойной чертой: .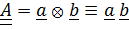

Далее знак (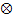) использовать не будем. На множестве диад вводятся правила:

1. Распределительный закон по отношению к первому и второму векторам:

.

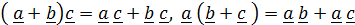2.Сочетательный закон по отношению к скалярному множителю:

.

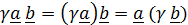3. Распределительный закон по отношению к скалярному множителю:

.

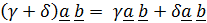4.Существование нулевой диады: .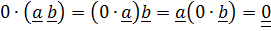

5. Под суммой двух и более диад будем понимать неупорядоченную совокупность .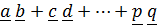

Рассматривая сумму двух диад 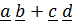, видим, что она не может быть записана в виде одной диады, за исключением случаев, сводящимся к правилам (1–3). Аналогично, нельзя свести к одной диаде и сумму б 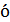льшего числа диад, т. е. правила (1–5) выводят нас за пределы множества диад (множество незамкнутое). Нетрудно убедиться, что минимальной неупрощаемой в общем случае совокупностью, к которой может быть приведена сумма любого числа диад, является сумма трех диад. Действительно, сумма, например, четырех диад в силу линейной зависимости в трехмерном пространстве четырех и более векторов записывается в виде суммы трех диад:

.

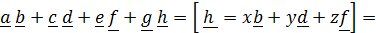
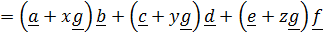Определение: Тензором второго ранга называется неупорядоченная сумма любого конечного числа диад .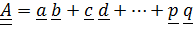

По поводу этого определения сделаем замечание. Тензор в виде одной диады иногда называют линейным тензором, в виде суммы двух диад – плоским, а в виде неупрощаемой суммы трех диад полным [1]. Смысл этих терминов станет понятным далее.