В каком бы виде ни был записан тензор поворота – через направляющие косинусы или в виде композиции поворотов, угол поворота и ось поворота определяются из выражений для следа и векторного инварианта тензора поворота: 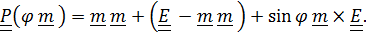
След и векторный инвариант
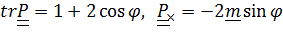 .
.
Рассмотрим композицию поворотов 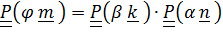 вокруг осей, заданных единичными векторами
вокруг осей, заданных единичными векторами 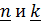 , угол между которыми равен
, угол между которыми равен 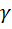 . Постараемся получить как можно более простые выражения для «суммарного» угла поворота
. Постараемся получить как можно более простые выражения для «суммарного» угла поворота 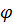 и оси поворота
и оси поворота 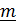 через углы
через углы 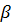 и
и 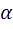 и оси
и оси 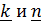 .
.
Перемножив тензоры и заменив в произведении диадные произведения скалярными и векторными, без труда найдем соответственно 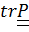 и
и 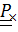 :
:
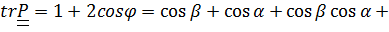
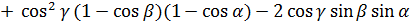 ,
,
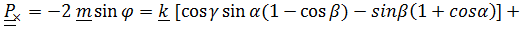
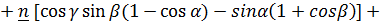
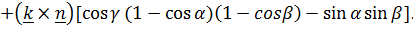
Эти выражения, приведенные в [3], можно упростить, перейдя в тригонометрических функциях к половинным углам.
Так, из выражения для 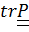 получим:
получим:
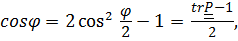
откуда, опуская элементарные (хотя и весьма громоздкие) выкладки, получим:
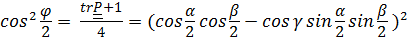 или
или
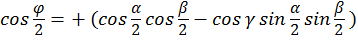 .(4.24)
.(4.24)
Аналогично, выражение для векторного инварианта преобразуется к виду:
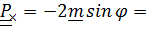
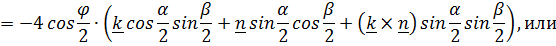
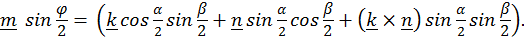 (4.25)
(4.25)
Формулы (4.24), (4.25), определяют угол и ось «суммарного» поворота. Они значительно проще приведенных в [5] громоздких и «малопривлекательных», по выражению П.А. Жилина, формул. Заметим, что знак (+) в (4.24) выбран из тех соображений, что если, например, 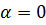 , то угол
, то угол 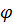 должен быть равен другому:
должен быть равен другому: 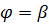 и
и 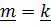 .
.
Если ввести векторы конечных поворотов Родрига [10]:
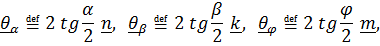
то формула (4.25) принимает форму правила сложения конечных поворотов: 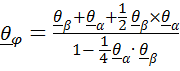 .
.
 2015-02-04
2015-02-04 525
525








