| S(t) |
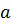
|
| A |
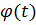
|
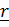
|
| Y |
| X |
| Z |
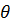
|
| R |
По полому кольцу, вращающемуся вокруг неподвижной, находящейся в плоскости кольца оси, движется точка. Найдем ее скорость и ускорение.
Применим теорему о сложении скоростей и ускорений, приняв кольцо за подвижную систему отсчета.
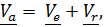
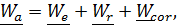 где
где 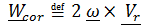 .
.
Уравнения будем проецировать на оси подвижной системы координат 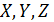 в подвижной системе отсчета, что, собственно, всегда и делается в учебных задачах, решаемых «графоаналитическим» способом с использованием неподвижного рисунка. Следует, конечно, помнить, что действительные векторы скорости и ускорения получаются поворотом найденных векторов вместе с подвижной системой:
в подвижной системе отсчета, что, собственно, всегда и делается в учебных задачах, решаемых «графоаналитическим» способом с использованием неподвижного рисунка. Следует, конечно, помнить, что действительные векторы скорости и ускорения получаются поворотом найденных векторов вместе с подвижной системой:
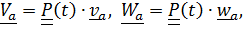
Вектор относительного положения точки
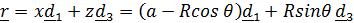 , где
, где 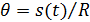 ;
;
вектор относительной скорости
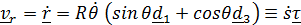 ,
,
где 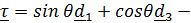 орт касательной к относительной траектории;
орт касательной к относительной траектории;
вектор переносной скорости
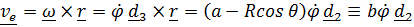 , где обозначено
, где обозначено 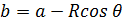 – расстояние от точки до оси вращения.
– расстояние от точки до оси вращения.
Таким образом, 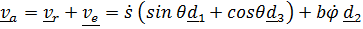 .
.
Если, как в этой задаче, траектория простая и ее орты касательной и нормали, а также радиус кривизны известны, вектор относительного ускорения можно найти или как сумму касательного (тангенциального) и нормального ускорений:
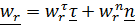 ,
,
где 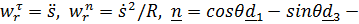 главная нормаль;
главная нормаль;
или, как в более сложных случаях, прямым дифференцированием:
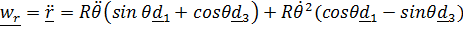 =
=
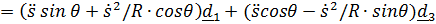 .
.
Вектор переносного ускорения
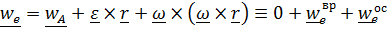 ,
,
где вращательное ускорение 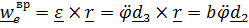 ,
,
а осестремительное 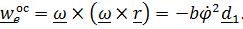
Ускорение Кориолиса
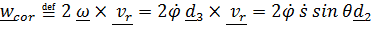 .
.
Таким образом,
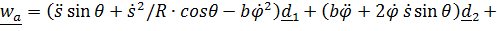
+ 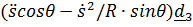 .
.
 2015-02-04
2015-02-04 356
356








