Тензор спина, вектор угловой скорости, формула Пуассона

Дифференцируя по времени уравнение 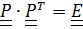, получим:

,

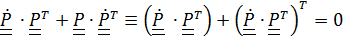или, обозначив 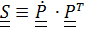: 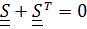. Тензор 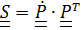, называемый тензором сп 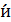на – кососимметричный, поэтому он может быть записан в виде (1.10):

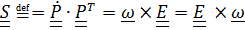, (4.13)

где 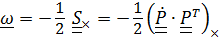называется вектором угловой скорости; прямая, параллельная вектору 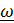, называется осью вращения. Прямым вычислением из представления Эйлера (4.11) можно получить формулу для вектора угловой скорости

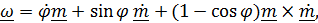(4.14)

из которой видно, что ось поворота, задаваемая вектором 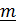, и ось вращения совпадают, только когда ось поворота неподвижна (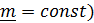, либо актуальное положение в данный момент времени совпадает с отсчетным 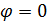; в этих случаях .

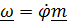Умножив равенство 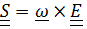справа скалярно на 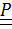, получим формулу Пуассона:

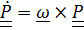. (4.15)