Рассматривается движение тела (ракеты) относительно двух систем отсчета – неподвижной с ортами 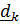 и подвижной с ортами
и подвижной с ортами 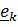 (рис. 4.13).
(рис. 4.13).
Необходимо определить абсолютную ориентацию тела по известной ориентации подвижной системы и относительной ориентации, информация о которой может быть передана в неподвижную систему любым способом, например, в виде телевизионной картинки или в числовом виде посредством направляющих косинусов 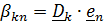 , измеряемых подвижным наблюдателем.
, измеряемых подвижным наблюдателем.
Тензор поворота, описывающий «абсолютную» ориентацию: 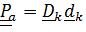 ,
, 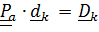 ; описывающий переносное движение:
; описывающий переносное движение: 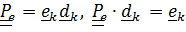 .
.
| Рис. 4.13.Сложное движение тела |
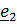
|
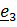
|
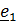
|
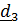
|
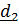
|
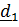
|
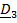
|
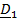
|
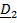
|
Тензор поворота относительной ориентации введем в виде:
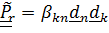 ,
, 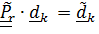 , т. е. этот тензор действительно описывает то движение, которое «видит» подвижный наблюдатель, одушевленный или неодушевленный (например, телекамера) и которое неподвижный может наблюдать на экране телевизора.
, т. е. этот тензор действительно описывает то движение, которое «видит» подвижный наблюдатель, одушевленный или неодушевленный (например, телекамера) и которое неподвижный может наблюдать на экране телевизора.
Таким образом,
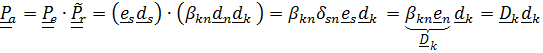 . (4.35)
. (4.35)
Вектор угловой скорости по теореме о сложении угловых скоростей имеет вид:
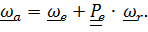 (4.36)
(4.36)
Вектор углового ускорения
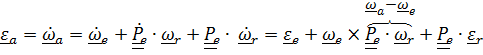 , или
, или
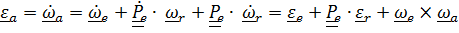 . (4.37)
. (4.37)
Существует и другая интерпретация [4] сложного движения, которая в описании ориентации по сути не отличается от изложенного подхода, а вот в части определения относительной угловой скорости отличается существенно.
Тензор поворота переносного движения, как и ранее, 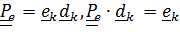 .
.
Тензором относительного поворота называется 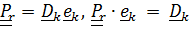 . Действительно, матрица компонент этого тензора, записанного в базисе
. Действительно, матрица компонент этого тензора, записанного в базисе 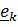 , описывает относительную ориентацию
, описывает относительную ориентацию 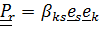 .
.
Очевидно, что тензор поворота абсолютного движения
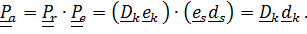
Сразу же отметим, что 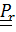 – это повернутый вместе с подвижной системой «истинный» тензор поворота относительного движения
– это повернутый вместе с подвижной системой «истинный» тензор поворота относительного движения 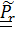 :
:
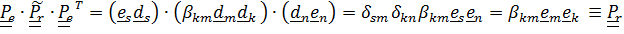 ,
,
так что 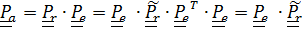 – формула (4.35).
– формула (4.35).
Векторы абсолютной и переносной угловых скоростей вводятся обычным способом в соответствии с формулой Пуассона: 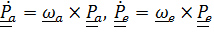 , а вот вектор относительной угловой скорости
, а вот вектор относительной угловой скорости 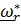 определяется таким образом, чтобы формула сложения угловых скоростей имела привычный (см. любой учебник) вид:
определяется таким образом, чтобы формула сложения угловых скоростей имела привычный (см. любой учебник) вид:
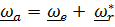 . (4.38)
. (4.38)
Для этого 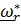 вводится формулой
вводится формулой
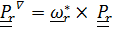 , (4.39)
, (4.39)
где 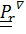 – производная Яуманна, известная в теоретической механике как относительная производная.
– производная Яуманна, известная в теоретической механике как относительная производная.
Так, если вектор задан координатами в подвижном базисе 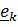 , то полная производная по времени имеет вид:
, то полная производная по времени имеет вид:
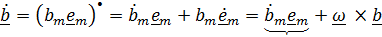 ,
,
где подчеркнутое слагаемое – относительная производная, т. е. производная, которую вычислял бы подвижный наблюдатель, для которого базисные векторы 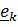 неподвижны.
неподвижны.
Таким образом, 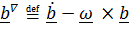 . Совершенно аналогично для тензора
. Совершенно аналогично для тензора
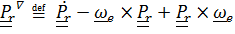 . (4.40)
. (4.40)
Дифференцируя 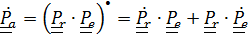 и заменяя
и заменяя 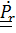 по (4.40), (4.39), придем к (4.38).
по (4.40), (4.39), придем к (4.38).
Собственно говоря, из (4.36) следует, что 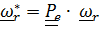 , т. е. это повернутый вместе с подвижной системой (вместе с телевизором) «истинный» вектор угловой скорости относительного движения
, т. е. это повернутый вместе с подвижной системой (вместе с телевизором) «истинный» вектор угловой скорости относительного движения 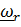 . При графоаналитическом решении задач, когда, разумеется, рассматривается актуальное состояние, именно
. При графоаналитическом решении задач, когда, разумеется, рассматривается актуальное состояние, именно 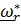 изображается на рисунках.
изображается на рисунках.
В качестве примера можно рассмотреть, например, вращающуюся вокруг неподвижной оси с ортом 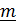 платформу, относительно которой вокруг оси с ортом
платформу, относительно которой вокруг оси с ортом 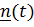 вращается тело (рис. 4.14).
вращается тело (рис. 4.14).
| Рис. 4.14. Сложное движение |
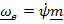
|
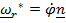
|
Введем подвижную систему отсчета, связанную с платформой. Тензор поворота переносного движения 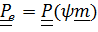 . Тензор поворота относительного движения («истинный»)
. Тензор поворота относительного движения («истинный») 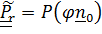 , где
, где 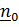 – орт оси поворота тела в отсчетном положении. Заметим, что для подвижного наблюдателя постоянный вектор
– орт оси поворота тела в отсчетном положении. Заметим, что для подвижного наблюдателя постоянный вектор 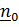 остается неподвижным и впредь. Разумеется, по (4.35),(4.36)
остается неподвижным и впредь. Разумеется, по (4.35),(4.36)
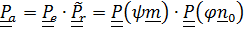 , (4.41)
, (4.41)
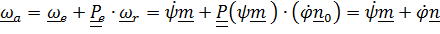 .
.
При втором подходе 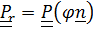 ,
, 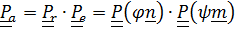 ,
, 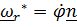 (вектор
(вектор 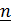 считается постоянным). Так как
считается постоянным). Так как 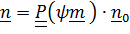 , то по теореме (4.12)
, то по теореме (4.12)
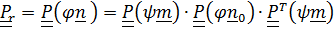 и, как отмечалось ранее, получим (4.41).
и, как отмечалось ранее, получим (4.41).
 2015-02-04
2015-02-04 432
432







