Теорема 4.2. Если тензор поворота 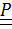 является композицией (произведением) поворотов
является композицией (произведением) поворотов 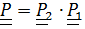 , то
, то
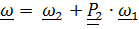 , (4.16)
, (4.16)
где 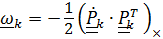 – угловые скорости, соответствующие тензорам
– угловые скорости, соответствующие тензорам 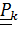 .
.
Доказательство. Докажем сначала лемму.
Пусть 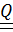 – тензор поворота,
– тензор поворота,  – произвольный тензор, тогда
– произвольный тензор, тогда
 , (4.17)
, (4.17)
т. е. векторный инвариант «повернутого» тензора равен «повернутому» векторному инварианту».
Доказательство леммы следует из тождества (1.15):
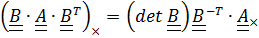 ,
,
в котором достаточно принять: 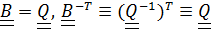 .
.
Впрочем, лемма имеет простой геометрический смысл. Примем в качестве  одну диаду
одну диаду 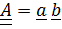 (в лемму тензор
(в лемму тензор  входит линейно). Пусть векторы
входит линейно). Пусть векторы 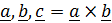 преобразуются тензором
преобразуются тензором 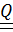 в
в 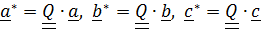 . Поскольку тройка поворачивается как жесткая система, то
. Поскольку тройка поворачивается как жесткая система, то 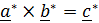 , т. е.
, т. е.
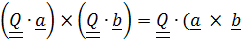 ) или
) или 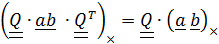 .
.
Вычисляя теперь тензор спина 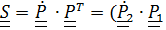 +
+ 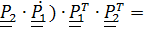
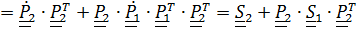
и сопутствующие векторы левой и правой частей с помощью леммы (4.17), получим (4.16).
Дифференцируя (4.16), получим формулу сложения угловых ускорений
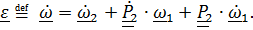
Заменив по формуле Пуассона 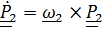 , получим
, получим
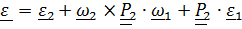 или, заметив, что
или, заметив, что 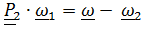 ,
,
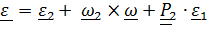
Упражнение 4.1. Показать, что если 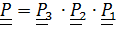 ,то
,то
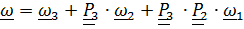
Практически во всех учебниках не дается строгого определения угловой скорости, это понятие остается «затененным» интуитивными соображениями (кроме фиксированной оси поворота, когда 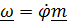 ). Доказываются «теоремы» о том, что
). Доказываются «теоремы» о том, что 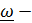 скользящий вектор, который «можно переносить вдоль оси вращения», что он не зависит от выбора полюса, что угловые скорости можно складывать, если тело вращается вокруг параллельных либо пересекающихся физических осей, но не рассматривается случай, когда оси не пересекаются и т. д. и т. п. Теорема сложения угловых скоростей всегда приводится в виде
скользящий вектор, который «можно переносить вдоль оси вращения», что он не зависит от выбора полюса, что угловые скорости можно складывать, если тело вращается вокруг параллельных либо пересекающихся физических осей, но не рассматривается случай, когда оси не пересекаются и т. д. и т. п. Теорема сложения угловых скоростей всегда приводится в виде 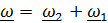 . Очевидно, что под
. Очевидно, что под 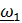 здесь понимается
здесь понимается 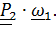
 2015-02-04
2015-02-04 1214
1214
