Теорема об изменении кинетической энергии. Пример

Скорость изменения кинетической энергии равна мощности внешних и внутренних воздействий:

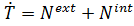. (5.44)

Эта теорема является следствием первого и второго фундаментальных законов механики.

Рассмотрим (для простоты) тело, состоящее из материальных точек.

Дифференцируя по времени кинетическую энергию

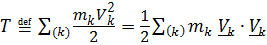, с учетом первого ФЗМ (для точки – второго закона Ньютона) получим:

.

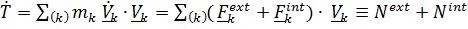Форма записи теоремы (5.44) называется дифференциальной; проинтегрировав ее, получим интегральную форму:

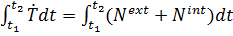, или

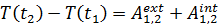(5.45)

Если все внутренние воздействия потенциальные, т. е. 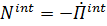, то (5.44) принимает вид

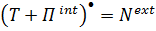, (5.46)

где сумма 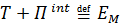называется полной механической энергией тела.

Если потенциальны и внешние воздействия 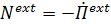, то имеем закон сохранения энергии расширенной системы (в энергию включается 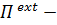потенциальная энергия воздействия на тело внешнего окружения):

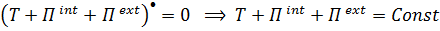. (5.47)

Системы (тела), где все воздействия потенциальны, называются консервативными.