Приведенная модель окружающего мира, описываемая двумя фундаментальными законами механики и их следствием – теоремой об изменении кинетической энергии, явно недостаточна. Нам мало известно о внутренних воздействиях, да и повседневный опыт показывает, что причинами движения тел являются не только силы и моменты, созданные окружающими телами, но и подвод энергии того или иного немеханического вида (тепловой, электрической и др.).
Рассмотрим простую задачу: два диска с осевыми моментами инерции 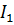 и
и 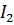 , вращающиеся соосно с разными угловыми скоростями
, вращающиеся соосно с разными угловыми скоростями 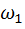 и
и 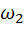 , в момент
, в момент 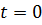 приводятся в зацепление и далее вращаются вместе с неизвестной угловой скоростью
приводятся в зацепление и далее вращаются вместе с неизвестной угловой скоростью 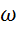 (рис. 5.17).
(рис. 5.17).
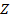
|
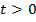
|
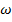
|
| A |
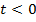
|
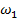
|
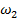
|
| Рис. 5.17. Сцепление дисков |
Проекция второго ФЗМ на ось вращения 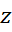 имеет вид:
имеет вид: 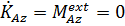 , т. е. проекция кинетического момента на ось
, т. е. проекция кинетического момента на ось 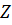 постоянна, отсюда находим:
постоянна, отсюда находим:
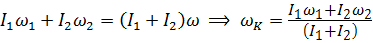 . (5.48)
. (5.48)
Найдем теперь угловую скорость с помощью теоремы об изменении кинетической энергии, тем более что она и выводилась из двух законов механики:
 ,
,
поскольку 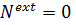 изначально, а равенство нулю
изначально, а равенство нулю 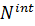 следует из того, что скорости точек касания сцепляющихся дисков одинаковы, а силы
следует из того, что скорости точек касания сцепляющихся дисков одинаковы, а силы 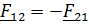 . Таким образом,
. Таким образом, 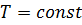 и
и
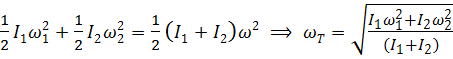 .
.
Разумеется, правильным результатом является формула (5.48). Найдем разность кинетических энергий после и до сцепления. Опуская несложные выкладки, получим:
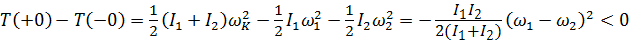 .
.
«Потерянная» энергия превратилась либо в тепловую энергию, либо стала энергией деформации дисков и валов. Все эти (и другие) варианты определяются свойствами тел.
В любом случае необходимо ввести в механику понятия внутренней энергии и подвода энергии в тело:
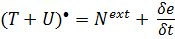 (5.49)
(5.49)
Скорость изменения полной энергии тела равна сумме мощности внешних воздействий и скорости подвода энергии в тело.
В (5.49) 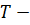 кинетическая энергия,
кинетическая энергия, 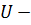 внутренняя энергия,
внутренняя энергия, 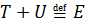 –полная энергия,
–полная энергия, 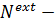 мощность внешних воздействий,
мощность внешних воздействий, 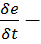 скорость подвода энергии в тело.
скорость подвода энергии в тело.
Если тело не обменивается энергией со своим окружением 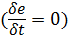 , оно называется замкнутым.
, оно называется замкнутым.
Понятие внутренней энергии успешно используется в механике деформируемых тел, в частности, для корректного введения векторов и тензоров деформации; в нашем же курсе внутренняя энергия встречается только как внутренняя потенциальная энергия 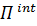 .
.
Глава 6. Механика Лагранжа
 2015-02-04
2015-02-04 313
313








