Пример

D

P

B

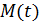
α

A

B

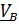
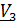
P

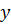
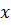
С помощью теоремы об изменении кинетической энергии в дифференциальной форме 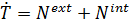составить дифференциальное уравнение, описывающее движение системы. При заданных 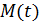и начальных условиях найти это движение.

За обобщенную координату примем угол поворота первого тела 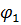. Сообщим системе обобщенную скорость 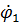и вычислим кинетическую энергию

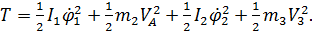
Кинематические соотношения имеют вид:

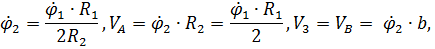
где обозначено .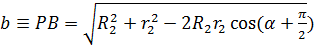

Кинетическая энергия записывается в виде

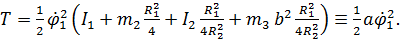
Мощность внутренних воздействий равна нулю, так как нити нерастяжимы, мощность внешних

,

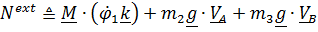или, с учетом ), ,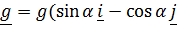

,

,

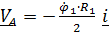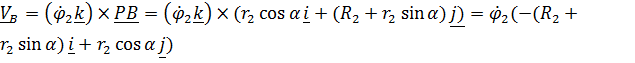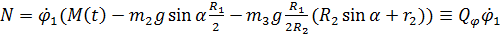где коэффициент 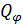при скорости в выражении мощности называют обобщенной силой.

Записывая теорему в дифференциальной форме, получим 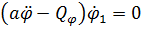, и, поскольку теорема справедлива для любых движений,

.

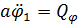В случае, когда приведенный инерционный коэффициент 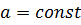(как в данном случае), интегрирование уравнения не вызывает трудностей.