Традиционно уравнения Лагранжа выводятся из уравнений Даламбера–Лагранжа для тел, состоящих из материальных точек, взаимодействие между которыми описываются только силами; хотя уравнения без какого–либо обоснования применяются для описания движения и твердых тел и твердых деформируемых тел, действие на тела-точки которых описывается силами и моментами, что влечет за собой необходимость введения наряду с возможными (виртуальными) перемещениями и возможных поворотов 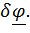 Это нетрудно сделать только для плоских движений, когда
Это нетрудно сделать только для плоских движений, когда 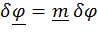 , где единичный вектор
, где единичный вектор 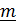 перпендикулярен плоскости движения.
перпендикулярен плоскости движения.
Вместе с тем следует заметить, что принцип Даламбера, опирающийся на первый фундаментальный закон изменения импульса (для точек–второй закон Ньютона) и на его обобщение для твердых тел – на второй (закон изменения кинетического момента) требует введения совершенно новых понятий: возможных, виртуальных и действительных перемещений и поворотов. Подобный подход способен создать у изучающего механику впечатление, что кроме фундаментальных законов необходимы еще какие–то добавочные «принципы».
Мы покажем, что уравнения Лагранжа следуют из записанной в обобщенных координатах теоремы об изменении кинетической энергии, которая на основе первого и второго законов легко доказывается для систем, состоящих из материальных точек и твердых тел, воздействия на которые описываются силами и моментами; она же, разумеется, является частным случаем третьего фундаментального закона баланса энергии.
Принимается следующее утверждение: нестационарных связей в общепринятой со времен Лагранжа форме 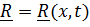 нет; явное присутствие времени в описании положения тела объясняется тем, что некоторые обобщенные координаты по необъясняемым причинам объявляются известными функциями времени.
нет; явное присутствие времени в описании положения тела объясняется тем, что некоторые обобщенные координаты по необъясняемым причинам объявляются известными функциями времени.
Обозначим все обобщенные координаты (в том числе и зависимости которых от времени объявляются известными) через 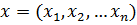 . Линейные скорости и угловые скорости являются однородными линейными функциями обобщенных скоростей
. Линейные скорости и угловые скорости являются однородными линейными функциями обобщенных скоростей
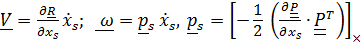 ,
,
и, поскольку общий вид кинетической энергии для точек и твердых тел имеет вид 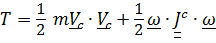 , то кинетическая энергия всей системы будет однородной квадратичной формой обобщенных скоростей:
, то кинетическая энергия всей системы будет однородной квадратичной формой обобщенных скоростей:
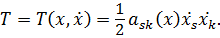 Тогда
Тогда
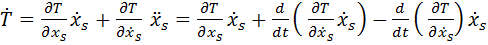 .
.
По теореме Эйлера об однородных функциях 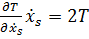 , следовательно,
, следовательно,
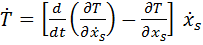 .
.
Мощность внешних и внутренних воздействий для материальных точек и твердых тел является однородной линейной формой обобщенных скоростей 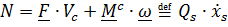 ,где коэффициенты при обобщенных скоростях по определению называются обобщенными силами.
,где коэффициенты при обобщенных скоростях по определению называются обобщенными силами.
Теорема об изменении кинетической энергии 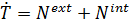 принимает вид:
принимает вид:
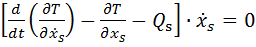
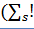 ). (6.1)
). (6.1)
Вследствие того, что теорема верна для всех движений, которые определяются произвольными начальными условиями и произвольными же обобщенными силами, и из-за независимости обобщенных скоростей (для голономных систем) все коэффициенты при скоростях равны нулю:
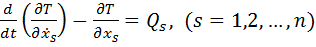 . (6.2)
. (6.2)
Это и есть система уравнений Лагранжа, которая с учетом начальных условий определяет действительное движение.
На первый взгляд может показаться, что перечисленных факторов произвольности и независимости скоростей недостаточно, чтобы каждая из скобок в сумме ( была равна нулю, поскольку внутри скобок имеются те же скорости.
была равна нулю, поскольку внутри скобок имеются те же скорости.
Заметим, что уравнение (6.1) получено на основе первых двух фундаментальных законов, а внутри скобок стоят скалярные произведения уравнений этих законов и независимых для голономных систем базисных векторов 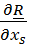 и
и 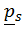 множества векторов положения материальных точек и тензоров поворота твердых тел, входящих в систему.
множества векторов положения материальных точек и тензоров поворота твердых тел, входящих в систему.
Рассмотрим тело, состоящее из материальных точек. Умножим каждое уравнение 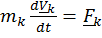 скалярно на
скалярно на 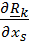 и просуммируем их:
и просуммируем их:
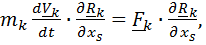
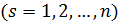 . (6.3)
. (6.3)
Справа в (6.3) стоит обобщенная сила 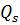 , а левая часть стандартным образом (см. например,
, а левая часть стандартным образом (см. например,  ) преобразуется с использованием тождеств Лагранжа, которые в нашем подходе из-за отсутствия времени в описании положения
) преобразуется с использованием тождеств Лагранжа, которые в нашем подходе из-за отсутствия времени в описании положения 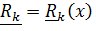 совершенно очевидны ввиду независимости смешанных производных от порядка дифференцирования:
совершенно очевидны ввиду независимости смешанных производных от порядка дифференцирования:
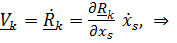
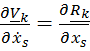 , и
, и 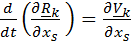 .
.
Имеем: 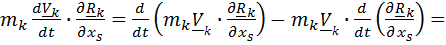
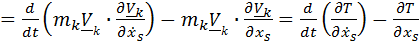 , (6.4)
, (6.4)
что и требовалось доказать.
С помощью тождеств типа Лагранжа для вращательных движений
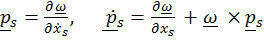 , (6.5)
, (6.5)
которые представлены далее, докажем справедливость аналогичного (6.4) преобразования для уравнения второго закона 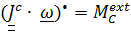 твердого тела:
твердого тела:
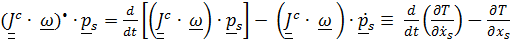 ,
,
где 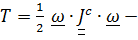 вращательная составляющая кинетической энергии.
вращательная составляющая кинетической энергии.
С учетом симметричности тензора инерции и первого тождества
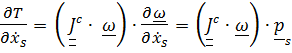 .
.
Вычислим 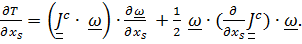 Выражая
Выражая 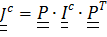 , где
, где 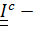 постоянный тензор инерции, получим:
постоянный тензор инерции, получим:
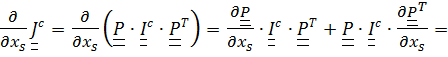
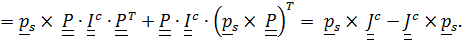
Теперь 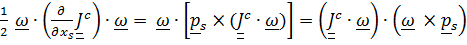 ,
,
и с учетом второго тождества получим:
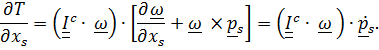
 2015-02-04
2015-02-04 510
510








