Следует подчеркнуть, что изложенный подход позволяет вычислять обобщенные силы (воздействия), которые обеспечивают постулируемую ранее зависимость некоторых координат от времени. Рассмотрим примеры.
Математический маятник с изменяющейся длиной (рис.6.2,а).
Материальная точка массы 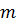 подвешена на нити, длина которой изменяется по закону
подвешена на нити, длина которой изменяется по закону 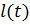 . Система имеет две обобщенные координаты:
. Система имеет две обобщенные координаты: 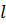 и
и 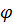 . Кинетическая энергия
. Кинетическая энергия 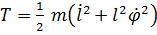 , мощность
, мощность
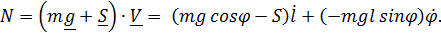
Уравнения Лагранжа 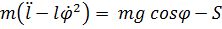 ;
; 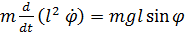 .
.
Из второго уравнения можно найти 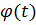 , из первого уравнения определяется натяжение нити
, из первого уравнения определяется натяжение нити 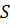 .
.
| Рис. 6.2. Постулируемая зависимость координат от времени |
| а) |
| S |
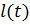
|
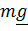
|
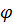
|
| б) |
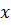
|
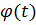
|
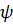
|
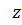
|
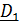
|
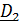
|
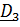
|
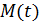
|
Движение диска по вращающемуся стержню (рис. 6.2,б). Диск массы
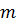 и радиуса
и радиуса 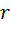 катится по вращающемуся стержню. Осевой момент инерции стержня
катится по вращающемуся стержню. Осевой момент инерции стержня 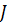 , жесткость пружины
, жесткость пружины 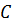 .
.
Система имеет две степени свободы  . Запишем уравнения Лагранжа:
. Запишем уравнения Лагранжа:
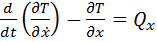 ,
, 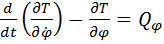 .
.
Сообщим находящейся в актуальном (т. е. произвольном) положении системе скорости 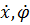 и напишем кинетическую энергию:
и напишем кинетическую энергию:
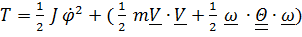 ,
,
где 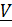 – скорость центра,
– скорость центра, 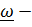 угловая скорость,
угловая скорость, 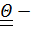 центральный тензор инерции диска.
центральный тензор инерции диска.
Приняв стержень за подвижную систему отсчета, получим
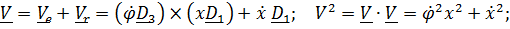
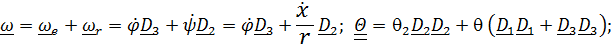
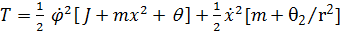 .
.
Обобщенные силы найдем «по определению» из выражения для мощности 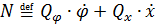 , причем ввиду независимости обобщенных скоростей можно для упрощения вычислений считать нулями все скорости кроме одной.
, причем ввиду независимости обобщенных скоростей можно для упрощения вычислений считать нулями все скорости кроме одной.
1. Примем 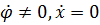 :
: 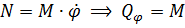 .
.
2. Примем 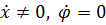 :
: 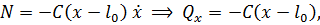
где 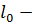 длина недеформированной пружины.
длина недеформированной пружины.
Уравнения Лагранжа будут иметь вид:
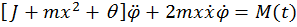 ;
;
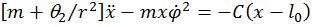 .
.
Рассмотрим частный случай движения, при котором стержень вращается с постоянной угловой скоростью 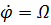 (именно этот случай чаще всего встречается в учебных задачах).
(именно этот случай чаще всего встречается в учебных задачах).
Второе уравнение запишем в виде
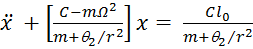 .
.
Для достаточно жесткой пружины 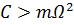 это уравнение описывает гармонические колебания:
это уравнение описывает гармонические колебания:
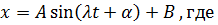
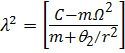 .
.
Первое уравнение дает нам значение момента, который необходим для вращения с постоянной угловой скоростью: 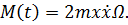
 2015-02-04
2015-02-04 581
581







