Не обращаясь к традиционному языку математики «(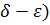 », скажем, что положение равновесия
», скажем, что положение равновесия 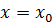 называется устойчивым по Ляпунову, если при достаточно малых начальных отклонениях и скоростях система не выйдет за пределы заданной сколь угодно малой окрестности положения равновесия.
называется устойчивым по Ляпунову, если при достаточно малых начальных отклонениях и скоростях система не выйдет за пределы заданной сколь угодно малой окрестности положения равновесия.
Теорема Лежен Дирихле об устойчивости. Если в положении равновесия 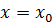 потенциальная энергия имеет строгий локальный минимум, то положение равновесия устойчиво по Ляпунову.
потенциальная энергия имеет строгий локальный минимум, то положение равновесия устойчиво по Ляпунову.
Кажется правдоподобным, что если в положении равновесия минимума 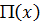 нет, то положение равновесия неустойчиво, но это в общем случае не доказано; существует множество частных теорем, из которых приведем одну:
нет, то положение равновесия неустойчиво, но это в общем случае не доказано; существует множество частных теорем, из которых приведем одну:
Теорема Ляпунова. Если в положении равновесия потенциальная энергия не имеет строгого локального минимума, причем это обстоятельство видно из разложения энергии в ряд, в котором сохранены только члены второго порядка, то положение равновесия неустойчиво.
Если потенциальная энергия – квадратичная форма: 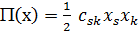 , то в случае ее положительной определенности положение равновесия устойчиво; если же нет – неустойчиво. Напомним, что квадратичная форма называется положительно определенной, если
, то в случае ее положительной определенности положение равновесия устойчиво; если же нет – неустойчиво. Напомним, что квадратичная форма называется положительно определенной, если 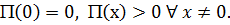 Ясно, что положительно определенная форма имеет в точке
Ясно, что положительно определенная форма имеет в точке 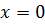 строгий локальный минимум, и, в соответствии с теоремой Дирихле, положение равновесия устойчиво; в противном случае локального минимума нет и в соответствии с теоремой Ляпунова положение равновесия неустойчиво.
строгий локальный минимум, и, в соответствии с теоремой Дирихле, положение равновесия устойчиво; в противном случае локального минимума нет и в соответствии с теоремой Ляпунова положение равновесия неустойчиво.
Из линейной алгебры известен критерий Сильвестра: Необходимым и достаточным условием положительной определенности квадратичной формы является положительность главных диагональных миноров и определителя матрицы, составленной из ее коэффициентов:
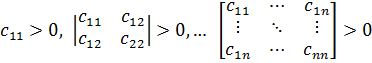 .
.
 2015-02-04
2015-02-04 618
618








