Общее решение строится как сумма главных колебаний с произвольными фазами, умноженных на произвольные постоянные:
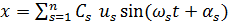 ,
,
или 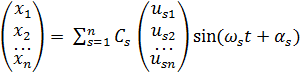 .
.
В общем решении 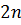 произвольных постоянных
произвольных постоянных 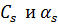 , которые можно найти из
, которые можно найти из 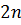 начальных условий
начальных условий 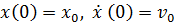 :
:
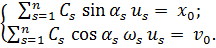
Обозначим 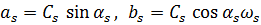 и перепишем систему в виде
и перепишем систему в виде
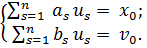
Определитель каждой из подсистем не равен нулю, поскольку его столбцы – линейно независимые формы колебаний. Постоянные 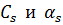 выражаются через
выражаются через 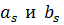 :
: 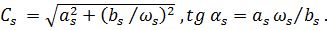
| Рис. 7.7. Свободные колебания |
 |
 |
 |
 |
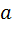 и массой
и массой 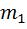 , к концу которого на тросе длиной
, к концу которого на тросе длиной 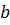 подвешен груз массы
подвешен груз массы 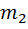 .(рис. 7.7). Устойчивость вертикального положения равновесия обеспечивается спиральной пружиной жесткостью
.(рис. 7.7). Устойчивость вертикального положения равновесия обеспечивается спиральной пружиной жесткостью 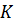 .
. Раскладывая потенциальную энергию в ряд до второй степени включительно, получим:
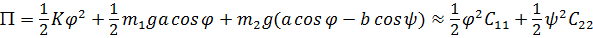 ,
,
где 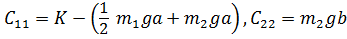 . Обобщенные силы:
. Обобщенные силы:
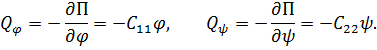
Кинетическая энергия, как уже отмечалось, записывается в момент прохождения системой положения равновесия:
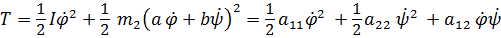 ,
,
где 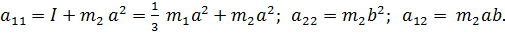
Уравнения Лагранжа имеют вид:
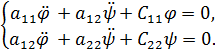
Решение этой системы будем искать в виде 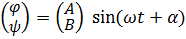 :
:
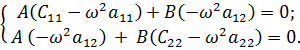
Приравнивая определитель нулю, получим частотное уравнение:
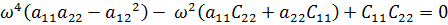 .
.
Пусть 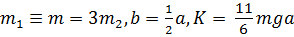 .
.
Тогда 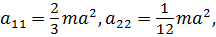
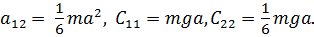
Частотное уравнение примет вид:
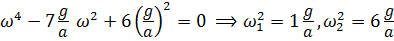 .
.
Отношение амплитуд найдем из первого, например, уравнения системы:
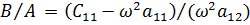 . Для первой собственной частоты
. Для первой собственной частоты 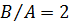 , для второй
, для второй 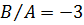 и общее решение имеет вид:
и общее решение имеет вид:
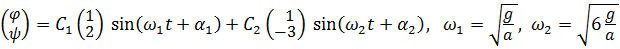 .
.
 2015-02-04
2015-02-04 774
774








