Дифференциальное уравнение имеет вид (7.1):  .
.
а ) Произвольное воздействие (интеграл Дюамеля). Возьмем для определенности малое сопротивление (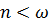 ). Полагая в решении (7.7г)
). Полагая в решении (7.7г) 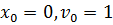 , получим движение с единичной начальной скоростью (реакцию системы на единичный импульс):
, получим движение с единичной начальной скоростью (реакцию системы на единичный импульс): 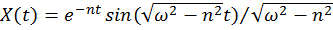 .
.
Движение при воздействии 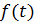 описывается интегралом Дюамеля:
описывается интегралом Дюамеля:
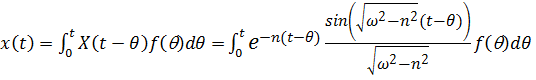 .
.
б) Гармоническое воздействие: дифференциальное уравнение имеет вид:
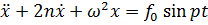 . (7.8)
. (7.8)
Частное решение, описывающее установившиеся колебания с частотой возмущающей силы, будем искать в виде 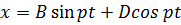 или, что одно и то же, в виде
или, что одно и то же, в виде 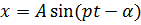 , где
, где 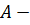 амплитуда колебаний;
амплитуда колебаний; 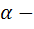 фаза.
фаза.
Подставляя это выражение в (7.8) и преобразовывая правую часть
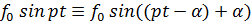 , получим:
, получим:
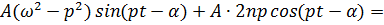
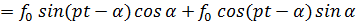 .
.
Приравнивая коэффициенты при 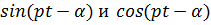 , получим:
, получим:
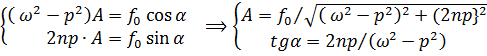 . (7.9)
. (7.9)
Зависимость амплитуды и фазы от частоты представлены на рис. 7.5. Максимальная амплитуда 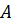 достигается при частоте
достигается при частоте 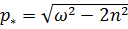 , при которой подкоренное выражение в знаменателе формулы (7.9) минимально.
, при которой подкоренное выражение в знаменателе формулы (7.9) минимально.
| Рис. 7.5. Зависимость амплитуды и фазы от частоты |
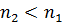
|
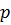
|
| A |
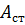
|
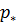
|
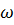
|
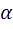
|
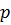
|
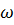
|
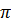
|

|
|
|
|
 2015-02-04
2015-02-04 483
483








