Руководствуясь тем, что ожидаемое движение имеет колебательный характер, частное решение системы (7.12) (или (7.13)) будем искать в виде:
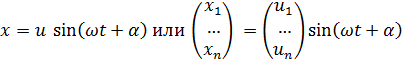 , (7.14)
, (7.14)
где вектор 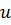 называется амплитудным вектором.
называется амплитудным вектором.
Подставляя (7.14) в систему (7.13), получим 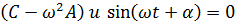 , откуда
, откуда
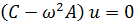 (7.15)
(7.15)
Чтобы однородная система (7.15) имела ненулевое решение 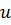 , необходимо, чтобы определитель этой системы был равен нулю:
, необходимо, чтобы определитель этой системы был равен нулю: 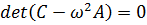 . Раскрывая определитель по степеням
. Раскрывая определитель по степеням 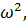 получим так называемое частотное уравнение
получим так называемое частотное уравнение 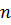 - ой степени относительно
- ой степени относительно 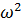 :
:
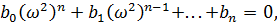 (7.16)
(7.16)
где, в частности, коэффициенты 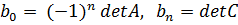 .
.
Стандартным в линейной алгебре способом, опирающимся на симметрию матриц 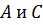 , можно показать, что все корни
, можно показать, что все корни 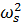 частотного уравнения вещественны, и, более того, если матрица жесткости
частотного уравнения вещественны, и, более того, если матрица жесткости 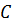 положительно определена (т. е. положение равновесия устойчивое), то корни положительные. В этом случае
положительно определена (т. е. положение равновесия устойчивое), то корни положительные. В этом случае 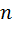 корней
корней 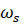 (c учетом их кратности) называются собственными частотами.
(c учетом их кратности) называются собственными частотами.
Ортогональность и линейная независимость форм колебаний. Подставив простую, т. е. кратности «один», собственную частоту 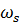 в систему (7.15), получим
в систему (7.15), получим 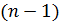 уравнений для
уравнений для 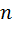 элементов амплитудного вектора
элементов амплитудного вектора 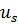 , поскольку при равенстве нулю определителя одно уравнение является линейной комбинацией остальных; поэтому из системы можно найти только отношения амплитуд к первой, например, амплитуде:
, поскольку при равенстве нулю определителя одно уравнение является линейной комбинацией остальных; поэтому из системы можно найти только отношения амплитуд к первой, например, амплитуде:
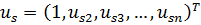 . (7.17)
. (7.17)
Амплитудный вектор (7.17), элементами которого являются отношения амплитуд, называется собственной формой колебаний. Колебания, описываемые выражением (7.14) при подстановке в него собственных частот 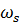 и форм
и форм 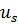 , называются главными колебаниями.
, называются главными колебаниями.
Покажем, что собственные формы колебаний, соответствующие различным частотам, ортогональны «с весом» матрицы инерции 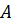 . Выпишем систему (7.15) для двух частот
. Выпишем систему (7.15) для двух частот 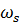 и
и 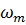
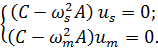 (7.18)
(7.18)
Первую из систем (7.18) умножим слева на 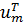 , а вторую на
, а вторую на 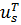 и вычтем:
и вычтем:
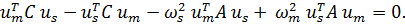
Учитывая симметричность 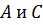 , получим:
, получим: 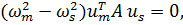 откуда получаем ортогональность собственных форм «с весом
откуда получаем ортогональность собственных форм «с весом 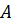 » или «в метрике А»:
» или «в метрике А»: 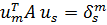 .
.
Заметим, что из ортогональности с весом 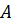 из (7.18) следует и ортогональность с весом
из (7.18) следует и ортогональность с весом  :
: 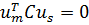 .
.
При частоте второй (для определенности) кратности равен нулю не только определитель системы (7.15), но и миноры порядка 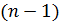 , т. е. имеется
, т. е. имеется 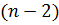 уравнения для
уравнения для 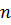 элементов амплитудного вектора, поэтому он имеет вид:
элементов амплитудного вектора, поэтому он имеет вид: 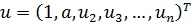 , где
, где 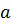 – произвольное число. Это обстоятельство позволяет для частоты второй кратности построить две собственные формы
– произвольное число. Это обстоятельство позволяет для частоты второй кратности построить две собственные формы 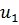 и
и 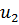 с числами
с числами 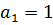 и
и 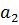 и найти
и найти 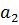 из условия ортогональности:
из условия ортогональности: 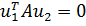 .
.
Из ортогональности форм следует их линейная независимость, т. е. равенство 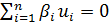 возможно тогда и только тогда, когда все
возможно тогда и только тогда, когда все 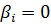 . Действительно, умножив эту сумму на матрицу
. Действительно, умножив эту сумму на матрицу 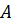 слева и потом на
слева и потом на 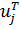 , получим с учетом ортогональности только одно слагаемое:
, получим с учетом ортогональности только одно слагаемое: 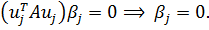
 2015-02-04
2015-02-04 1561
1561
