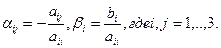 (2.5)
(2.5)
Перепишем систему (2.4) с учетом введенных обозначений
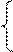 x1=α12x2+α13x3+β1
x1=α12x2+α13x3+β1
x2=α21x1+α23x3+β2 (2.6)
x3=α31x1+α32x2+β3
Систему (2.6) будем решать методом последовательных приближений. Выбираем произвольно начальное приближение к решению системы
x(0)=(x10, x20, x30). (2.7)
Подставив в (2.6) получим новое приближение x(1):
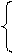 x11=α12x20+α13x30+β1
x11=α12x20+α13x30+β1
x21=α21x10+α23x30+β2 (2.8)
x31=α31x10+α32x20+β3
Этим заканчивается первая итерация. На втором шаге начальные приближения х10, х20, х30 заменяются на х11, х21, х31 и процесс (2.8) повторяется вновь для вычисления второго приближения х(2)=(х12, х22, х32) и т. д.
Итерационный процесс продолжается до тех пор, пока все xi(k+1) не станут достаточно близки к хi(k). Критерий близости между х(k) и x(k+1) приближениями оцениваются по формуле
||x(k+1)-x(k)|| 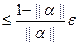 (2.9)
(2.9)
где ||x(k+1)-x(k)||- норма вектора разностей;
||α||- одна из норм матрицы α системы (2.8);
ε – заданная погрешность.
Пример. Решить систему
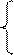 3.5x1+1.2x2-0.5x3=5,
3.5x1+1.2x2-0.5x3=5,
0.1x1+5x2+2x3=11, (2.10)
2x1-0.3x2+7x3=14.
Приведем систему к эквивалентному виду (2.6).
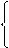 х1=-0.34х2+0.14х3+1.42,
х1=-0.34х2+0.14х3+1.42,
х2=-0.02х1-0.4х3+2.2, (2.11)
х3=-0.29х1+0.04х2+2.
За начальное приближение корней системы (2.11) принимаем произвольные значения: х10=1; х20=2; х30=2.
Подставляем эти значения в правые части уравнений (2.11).
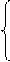 х11=-0,34*2+0.14*2+1.42=1.02,
х11=-0,34*2+0.14*2+1.42=1.02,
х21=-0.02*1-0.4*2+2.2=1.42, (2.12)
х31=-0.29*1+0.04*2+2=2.21.
Пусть погрешность метода ε=0.01. Определим норму вектора разностей.
||x(1)-x(0)||=max 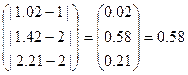 (2.13)
(2.13)
Определим одну из норм матрицы α, введя нулевые коэффициенты на главной диагонали:
 0 -0.34 0.14
0 -0.34 0.14
α=-0.02 0 -0.4, (2.14)
-0.29 0.04 0
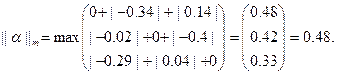 (2.15)
(2.15)
С помощью (2.9) проверим условие окончания процесса итерации.
0.58 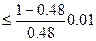 (2.16)
(2.16)
Условие не выполняется, процесс итерации следует повторить.
Сходимость процесса итерации возможна только для определенного класса систем уравнений.
Приведем без доказательства достаточное условие сходимости.
Если для эквивалентной системы (2.8) выполнено по крайней мере одно из условий
1. 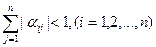
2. 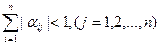
т. е. одна из норм матрицы α меньше 1, то процесс итерации (2.9) сходится к единственному решению этой системы, независимо от выбора начального приближения.
Следствие. Для системы (2.3) метод итерации сходится, если выполнены неравенства
|aij|> 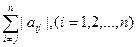 . (2.17)
. (2.17)
Т. е. если модули диагональных коэффициентов для каждого уравнения системы больше суммы модулей всех остальных коэффициентов.
Теорема сходимости накладывает жесткие условия на коэффициенты данной линейной системы.
Например.
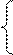 x1-4x2+x3=3 1)
x1-4x2+x3=3 1)
2x1+3x2-0.5x3=5 2)
-4x1+1.5x2-3.5x3=7 3)
Система не отвечает условиям теоремы сходимости: следствие теоремы сходимости не выполняется. Однако, если detA≠0, то с помощью линейного комбинирования уравнений системы последнюю можно привести к виду, удобному для итераций.
Выполним следующие преобразования: в первом уравнении коэффициент при х2 по модулю больше суммы модулей остальных коэффициентов, примем данное уравнение за второе уравнение системы. Первое уравнение получим, суммируя первое и второе уравнения, третье получим суммируя все три уравнения системы. В линейной комбинации должны участвовать все уравнения исходной системы. Получим
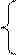 3x1-x2+0.5x3=8 1)+2)
3x1-x2+0.5x3=8 1)+2)
x1-4x2+x3=3
-x1+0.5x2-3x3=15 1)+2)+3)
Новая система отвечает условиям теоремы сходимости, следовательно, можно применить метод итераций.
 2015-02-27
2015-02-27 704
704








