Линейным дифференциальным уравнением первого порядка называется уравнение вида
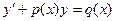 (5)
(5)
Однородным линейным дифференциальным уравнением первого порядка называется уравнение
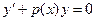 , (6)
, (6)
Которое получается из (5) при q(x)=0. это уравнение является уравнением с разделяющимися переменными и интегрируется.
Решения уравнения (5) ищутся в виде произведения двух неизвестных функций y = u(x)× v(x). Так как 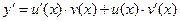 , то из (5) следует,
, то из (5) следует, 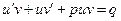 или
или
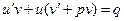 . (7)
. (7)
Выберем функцию v=v(x) такой, чтобы выполнялось равенство
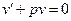 (8)
(8)
Это можно сделать, решая уравнение (8) с разделяющимися переменными. После выбора функции v=v(x) уравнение (7) примет вид 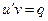 . Это уравнение также является уравнением с разделяющимися переменными. Интегрируя его, находим функцию u=u(x). Тогда функция y=u(x)v(x) будет решением уравнения (5).
. Это уравнение также является уравнением с разделяющимися переменными. Интегрируя его, находим функцию u=u(x). Тогда функция y=u(x)v(x) будет решением уравнения (5).
Таким образом, интегрирование линейного дифференциального уравнения первого порядка сводится к интегрированию двух уравнений с разделяющимися переменными.
Пример:
Решить уравнение 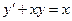 .
.
Решение будем искать в виде y=uv. Подставляя y=uv и 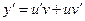 в уравнение, получим
в уравнение, получим 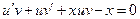 или
или 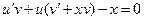 .
.
Запишем уравнение 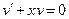 в виде
в виде
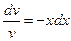 .
.
Отсюда
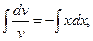
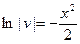 ,
, 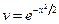 .
.
Теперь решаем уравнение 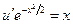 , которое запишем в виде
, которое запишем в виде 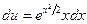 и проинтегрируем:
и проинтегрируем:
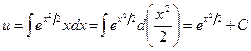 .
.
Итак, общее решение данного уравнения имеет вид
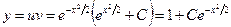 .
.
 2015-02-04
2015-02-04 327
327








