2015-02-04
381
Знакоположительным называется такой числовой ряд, все члены которого положительны.
Первый признак сравнения(признак сравнения в непредельной форме).
Пусть даны два ряда с положительными членами:
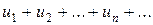(4)
и
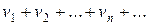, (5)
причем каждый член ряда (4) не превосходит соответствующего члена ряда (5), т.е.
, 
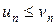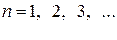. (6)
Тогда если сходится ряд (5), то сходится и ряд (4); если расходится ряд (4), то расходится и ряд (5).
Этот признак справедлив и для случая, когда условие (6) начинает выполняться не при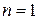 
, а с любого значения номера 
.
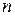Второй признак сравнения(признак сравнения в предельной форме).
Пусть для рядов (4) и (5) существует предел
.
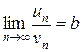Тогда если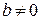 
, то либо оба ряда сходятся, либо оба ряда расходятся; если 
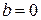и ряд (5) сходится, то сходится и ряд (4). Если же
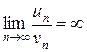
и ряд (5) расходится, то расходится и ряд (4).
Ряды, сходимость или расходимость которых полезно запомнить для применения признаков сравнения.
Гармонический ряд: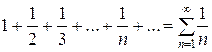 
; этот ряд расходится.
Обобщенный гармонический ряд (или ряд Дирихле):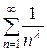 
; этот ряд расходится при 
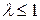и сходится при 
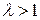. Рассмотренный выше гармонический ряд является частным случаем ряда Дирихле при 
.
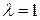Признак Даламбера.
Если для ряда с положительными членами
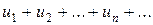
существует предел отношения последующего члена к предыдущему
,
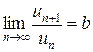то этот ряд сходится при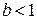 
и расходится при 
.
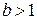При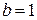 
возможны оба случая, т.е. исследование такого ряда по признаку Даламбера не дает однозначного ответа на вопрос о сходимости.
Радикальный признак Коши.
Если для ряда с положительными членами
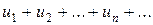
существует предел
,
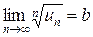то этот ряд сходится, если 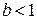, и расходится, если .
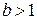При 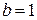возможны оба случая, т.е. исследование такого ряда по радикальному признаку Коши не дает однозначного ответа на вопрос о сходимости.
Интегральный признак Коши.
Ряд с положительными членами
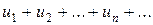, (7)
где 
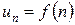, и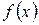 
- непрерывная монотонно убывающая при 
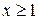функция, сходится, если сходится несобственный интеграл
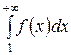. (8)
Если же интеграл (8) расходится, то расходится и ряд (7).
