Уравнения с разделяющимися переменными

Решение уравнений вида (2) сводится к нахождению неопределенных интегралов, если функция двух переменных f(x,y) представима в виде произведения двух функций одной переменной

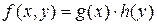
Заменяя 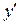на 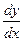, из (2) получаем

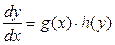(3)

Уравнением с разделяющимися переменными называется уравнение вида (3).

По-другому такие уравнения можно записать в виде

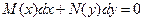(4)

или

.

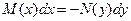Интегрируя обе части последнего равенства, получаем

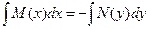
Пример.

Решить уравнение .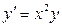

Дифференциальное уравнение запишем в виде

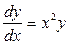, или .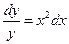

После интегрирования получим

, .

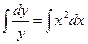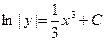Отсюда

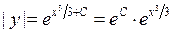или ,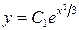

где 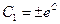− произвольная постоянная.