Линейным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида
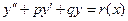 (9)
(9)
где p, q − некоторые числа, r(x) − функция от x.
Однородным линейным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение (9), в котором правая часть r(x) равна нулю:
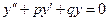 (10)
(10)
Общее решение уравнения (9) равно сумме какого-либо частного решения этого уравнения и общего решения соответствующего однородного уравнения (10).
Опишем сначала способ нахождения общего решения однородного уравнения (10).
Характеристическим уравнением для однородного уравнения называется квадратное уравнение
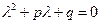 (11)
(11)
относительно неизвестной 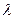 .
.
В соответствии со знаком дискриминанта 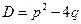 возможны три случая:
возможны три случая:
1) D>0. Тогда характеристическое уравнение имеет два различных корня 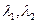 ;
;
2) D=0. Тогда характеристическое уравнение имеет один корень 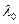 ;
;
3) D<0. Тогда действительных корней характеристическое уравнение не имеет. В этом случае находятся числа 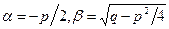 .
.
Найдем общее решение уравнения (10) для всех этих случаев.
1) Если характеристическое уравнение (11) имеет два различных корня 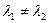 , то общее решение уравнения (10) имеет вид
, то общее решение уравнения (10) имеет вид
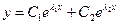 (12)
(12)
где С1, С2 − произвольные постоянные.
2) Если характеристическое уравнение (11) имеет единственный корень 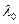 , то общее решение уравнения (10) имеет вид
, то общее решение уравнения (10) имеет вид
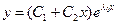 , (13)
, (13)
где С1, С2 − произвольные постоянные.
3) Если характеристическое уравнение не имеет корней, то общее решение уравнения (10) имеет вид
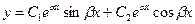 , (14)
, (14)
где С1, С2 − произвольные постоянные.
Примеры:
1. Для уравнения 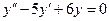 характеристическое уравнение имеет вид
характеристическое уравнение имеет вид 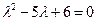 . Его различными корнями являются числа
. Его различными корнями являются числа 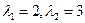 . Поэтому общее решение данного уравнения
. Поэтому общее решение данного уравнения
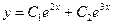 .
.
2. Для уравнения 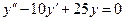 характеристическое уравнение имеет вид
характеристическое уравнение имеет вид 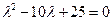 . Число
. Число 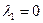 является его единственным корнем. Поэтому общее решение данного уравнения записывается в виде
является его единственным корнем. Поэтому общее решение данного уравнения записывается в виде
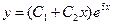 .
.
3. Для уравнения 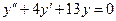 характеристическое уравнение
характеристическое уравнение 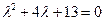 не имеет корней. Находим числа
не имеет корней. Находим числа 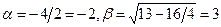 . Поэтому общее решение данного уравнения
. Поэтому общее решение данного уравнения
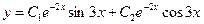 .
.
Способы нахождения частных решений неоднородных уравнений (9) зависит от вида правой части и в явном виде находятся только для функций r(x) специального вида.
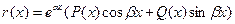 (15)
(15)
где 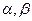 −некоторые числа, причем
−некоторые числа, причем 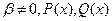 − многочлены от х.
− многочлены от х.
В этом случае частное решение уравнения (9) ищется в виде
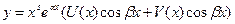 (16)
(16)
где U(x), V(x) − многочлены, степени которых равны наибольшей из степеней многочленов P(x) и Q(x). При этом показатель s выбирается по следующему правилу:
1) s = 0, если
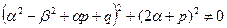 (17)
(17)
2) s = 1, если
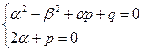 (18)
(18)
Многочлены U(x) и V(x) указанной степени в формуле (16) записываются в общем виде с постоянными коэффициентами. Затем находятся производные 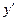 и
и 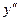 функции (16). После подстановки
функции (16). После подстановки 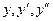 в уравнение (9) получается линейная система уравнений для определения коэффициентов многочленов U(x) и V(x).
в уравнение (9) получается линейная система уравнений для определения коэффициентов многочленов U(x) и V(x).
Примеры:
1. найти частное решение уравнения
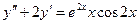 .
.
Здесь 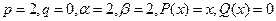 , наибольшая степень полиномов P(x) и Q(x) равна 1. поскольку
, наибольшая степень полиномов P(x) и Q(x) равна 1. поскольку 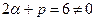 , то условие (17) выполняется, поэтому s = 0. Решение (16) будем искать в виде
, то условие (17) выполняется, поэтому s = 0. Решение (16) будем искать в виде
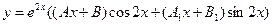 .
.
Найдем производные:
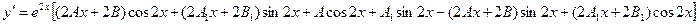 или
или
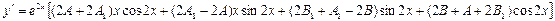 .
.
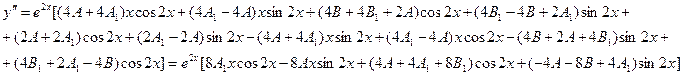
Подставляя полученные значения функции у и ее производной в исходное уравнение и приравнивая коэффициенты в левой и правой частях при функциях 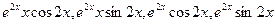 , получаем систему линейных уравнений:
, получаем систему линейных уравнений:
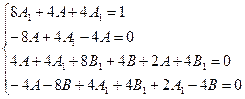
Отсюда
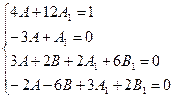
Решением этой системы будут числа
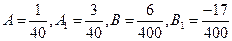 .
.
Таким образом, частное решение исходного уравнения имеет вид
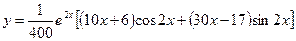
2. найти частное решение уравнения
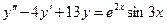
Здесь 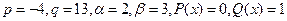 , наибольшая степень полиномов P(x) и Q(x) равна 0.
, наибольшая степень полиномов P(x) и Q(x) равна 0.
Поскольку 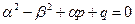 и
и 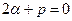 , то условия (18) выполнены. Поэтому в (16) показатель s = 1, и частное решение ищем в виде
, то условия (18) выполнены. Поэтому в (16) показатель s = 1, и частное решение ищем в виде
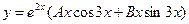 .
.
Находим производные:
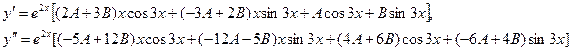
Подставляя полученные значения 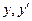 и
и 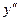 в исходное уравнение и приравнивая коэффициенты в правой и левой частях при функциях
в исходное уравнение и приравнивая коэффициенты в правой и левой частях при функциях 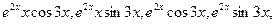 получаем систему линейных уравнений:
получаем систему линейных уравнений:
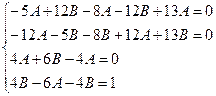
Из этой системы находим 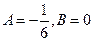 .
.
Таким образом, частное решение исходного уравнения имеет вид
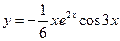 .
.
Пусть теперь правая часть уравнения (9) имеет вид:
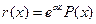 (19)
(19)
где 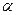 − некоторое число, P(x) − многочлен от х (этот случай получается из (15) при
− некоторое число, P(x) − многочлен от х (этот случай получается из (15) при 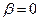 ).
).
Частное решение уравнения (9) ищется в виде
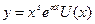 (20)
(20)
Где U(x) − многочлен с неопределёнными коэффициентами, степень которого равна степени многочлена P(x). При этом показатель s выбирается по следующему правилу:
1) s = 0, если
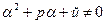 (21)
(21)
2) s = 1, если
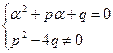 (22)
(22)
1) s = 0, если
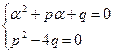 (23)
(23)
Примеры:
1. найти частное решение уравнения
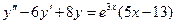 .
.
Здесь p = - 6, q = 8, 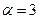 , P(x) = 5x – 13. поскольку
, P(x) = 5x – 13. поскольку 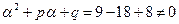 , то показатель s в (20) равен 0. Частное решение ищем в виде
, то показатель s в (20) равен 0. Частное решение ищем в виде
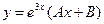 .
.
Находим производные:
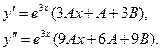
Подставляя 
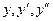 в исходное уравнение и приравнивая коэффициенты в левой и правой частях при функциях
в исходное уравнение и приравнивая коэффициенты в левой и правой частях при функциях 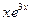 и
и 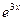 , получим систему линейных уравнений
, получим систему линейных уравнений
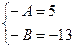
Отсюда А=-5, В=13, и искомое частное решение имеет вид
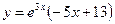 .
.
Ряды.
 2015-02-04
2015-02-04 4349
4349
