П.1. Основные понятия о числовых рядах и определения

Числовой последовательностью называется упорядоченный набор нумерованных чисел 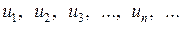, представляющая собой функцию

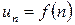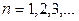, (1)

заданную на множестве натуральных чисел. Числа 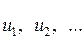называются соответственно первым, вторым и так далее членами последовательности. Число 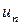, задаваемое формулой (1), называется общим членом последовательности.

В последовательностях и рядах широко используется функция натурального аргумента

,

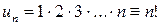представляющая собой произведение первых 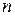натуральных чисел. Обозначение 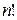читается как «эн факториал».

Пусть u₁, u₂, u₃,…, u_n,…, где u_n = f(n), - бесконечная числовая последовательность. Тогда выражение

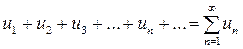
(2)

называется числовым рядом.

Числа 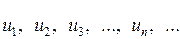называются членами ряда. При этом

,

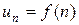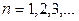
называется общим членом ряда. Ряд считается заданным, если задана формула для 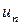. Нумерация членов ряда, вообще говоря, может начинаться с любого целого числа.

Сумму первых членов ряда по n -ный включительно обозначают S_n и называют n -ной частичной суммой ряда, т.е.

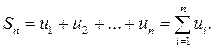
Сумму остальных слагаемых, начиная с 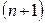- го, называют n-ным остатком числового ряда и обозначают 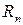, т.е.

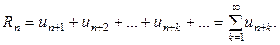
Согласно определению (2), остаток числового ряда можно рассматривать как самостоятельный числовой ряд.

Предел последовательности 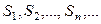частичных сумм при 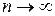, если он существует, называется суммой ряда и обозначается буквой S, т.е.

.

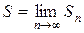Если 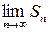существует, т.е. если сумма S есть конечное число, то говорят, что ряд (2) сходится. В противном случае говорят, что ряд (2) расходится.

Частный случай числового ряда – геометрический ряд, представляющий собой сумму бесконечной геометрической прогрессии:

.

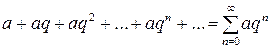Его частичная сумма:

.

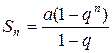При этом если 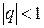, то геометрическая прогрессия называется бесконечно убывающей, и геометрический ряд имеет конечную сумму

.

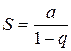В случаях, когда 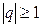, геометрический ряд расходится, т.е. конечной суммы не имеет.