Полным приращением функции двух переменных z = f (x, y) в точке (x, y), вызванным приращениями аргументов 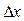 и
и 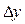 , называется выражение
, называется выражение 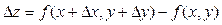 .
.
Функция z = f (x, y) называется непрерывной в точке (x, y), если бесконечно малым приращениям аргументов соответствует бесконечно малое полное приращение функции.
Если обозначить 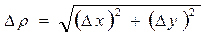 – расстояние между близкими точками
– расстояние между близкими точками 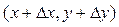 и (х, у), то
и (х, у), то 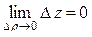 – это определение непрерывности ФНП на языке приращений.
– это определение непрерывности ФНП на языке приращений.
Если функция z = f (x, y) непрерывна в любой точке (х, у)Î D, то она называется непрерывной ФНП в области D.
Функция z = f (x, y), полное приращение Dz которой в данной точке (x,y) может быть представлено в виде суммы двух слагаемых: выражения, линейного относительно 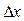 и
и 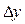 , и величины, бесконечно малой более высокого порядка малости относительно
, и величины, бесконечно малой более высокого порядка малости относительно 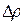 , называется дифференцируемой ФНП в данной точке, а линейная часть ее полного приращения называется полным дифференциалом ФНП.
, называется дифференцируемой ФНП в данной точке, а линейная часть ее полного приращения называется полным дифференциалом ФНП.
Если 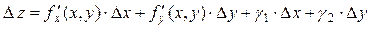 , где
, где 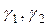 –бесконечно малые при
–бесконечно малые при 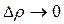 , то полный дифференциал функции z = f (x, y) выражается формулой:
, то полный дифференциал функции z = f (x, y) выражается формулой: 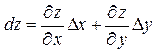 , или:
, или:
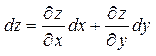 (1)
(1)
(приращения независимых переменных совпадают с их дифференциалами: D х = dx, D y = dy).
Из определения полного дифференциала следует его связь с полным приращением: при малых 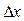 и
и 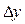 полное приращение функции D z примерно равно ее полному дифференциалу:
полное приращение функции D z примерно равно ее полному дифференциалу: 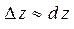 с точностью до бесконечно малых более высокого порядка малости относительно
с точностью до бесконечно малых более высокого порядка малости относительно 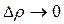 .
.
Полный дифференциал функции z = f (x, y) зависит как от точки M (x 0, y 0), в которой он вычисляется, так и от приращений 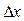 и
и 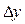 .
.
 2015-02-04
2015-02-04 2719
2719
