П.8. Нахождение наибольшего и наименьшего значений ФНП в замкнутой области

Область D называется замкнутой областью, если она включает в себя свою границу, и открытой областью, если не включает свою границу.

По свойствам непрерывных функций, непрерывная ФНП z = f (x, y) в замкнутой ограниченной области D 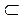xOy достигает своих наибольшего и наименьшего значений z_наиб = М_. и z_наим = m, называемых глобальными экстремумами ФНП в области D. Эти значения z_наиб. и z_наим. достигаются или в точках локальных экстремумов функции z = f (x, y) внутри области D или на границе этой области.

Чтобы найти наибольшее и наименьшее значения дифференцируемой ФНП в замкнутой ограниченной области D, нужно:

1) найти все стационарные точки функции f (x, y), лежащие внутри области D, и вычислить в них значения функции;

2) найти наибольшее и наименьшее значения функции на границе области;

3) выбрать среди всех найденных значений наибольшее и наименьшее значения функции в области D.

Поскольку на границе области аргументы x и y связаны между собой уравнением границы, то граничное значение функции f (x, y) является функцией одной переменной, и ее исследование проводят по правилам нахождения наибольшего и наименьшего значений функции одной переменной на замкнутом промежутке.

Если граница области D является кусочно-заданной, то необходимо исследовать граничное значение функции f (x, y) отдельно на каждом участке границы.