Говорят, что в двумерной области D 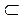 xOy задано скалярное поле, если в каждой точке M(x,y) Î D задана скалярная функция координат точки:
xOy задано скалярное поле, если в каждой точке M(x,y) Î D задана скалярная функция координат точки:
U(M) = U(x,y).
Пример: скалярное поле температур T(x,y) в области D.
Линии уровня скалярного поля – это такие линии, на каждой из которых функция U(x,y) сохраняет постоянное значение.
Уравнения линий уровня скалярного поля: U (x, y) = const.
Геометрически линии уровня получаются, если поверхность z = U(x,y) пересекать горизонтальными плоскостями z = С и проектировать линии пересечения на плоскость xOy.
Градиентом скалярного поля U (x, y) в фиксированной точке 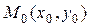 называется вектор, проекции которого на оси координат совпадают с частными производными функции, вычисленными в точке М0:
называется вектор, проекции которого на оси координат совпадают с частными производными функции, вычисленными в точке М0:
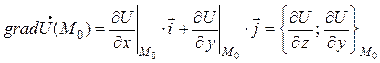 , (7)
, (7)
где векторы 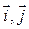 – это орты координатных осей.
– это орты координатных осей.
Вектор градиента 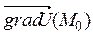 направлен перпендикулярно касательной к линии уровня, проходящей через точку М0. Направление градиента указывает направление наибольшего роста функции U(x,y) в точке М 0.
направлен перпендикулярно касательной к линии уровня, проходящей через точку М0. Направление градиента указывает направление наибольшего роста функции U(x,y) в точке М 0.
Отложим от фиксированной точки M 0(x 0, y 0) некоторый вектор 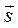 .
.
Скорость изменения скалярного поля U(x,y) в направлении вектора 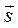 характеризует величина
характеризует величина 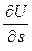 , называемая производной по направлению.
, называемая производной по направлению.
Если в прямоугольной системе координат xОy вектор 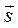 имеет направляющие косинусы cos a иcos b, то производная функции U(x,y) по направлению вектора
имеет направляющие косинусы cos a иcos b, то производная функции U(x,y) по направлению вектора 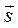 в точке М 0 – число
в точке М 0 – число 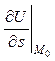 – можно найти по формуле:
– можно найти по формуле:
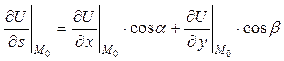 , (8)
, (8)
Напомним формулы для вычисления направляющих косинусов вектора 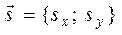 :
:
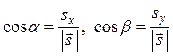 , где модуль вектора:
, где модуль вектора: 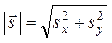 .
.
Аналогично определяют скалярное поле U(M) в трехмерной области V:
U(M) = U(x,y,z), 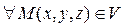 . Поверхности уровня скалярного поля – это такие поверхности, на каждой из которых функция U(x,y,z) сохраняет постоянное значение. Уравнения поверхностей уровня скалярного поля: U(x,y,z) = const.
. Поверхности уровня скалярного поля – это такие поверхности, на каждой из которых функция U(x,y,z) сохраняет постоянное значение. Уравнения поверхностей уровня скалярного поля: U(x,y,z) = const.
Градиент скалярного поля U(x,y,z) в произвольной точке M (x, y, z):
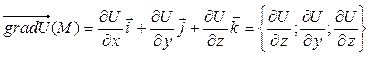 , (9)
, (9)
где векторы 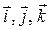 – это орты координатных осей.
– это орты координатных осей.
Вектор 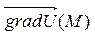 поля U(x,y,z) направлен параллельно нормали к поверхности уровня U(x,y,z) = const в точке М.
поля U(x,y,z) направлен параллельно нормали к поверхности уровня U(x,y,z) = const в точке М.
 2015-02-04
2015-02-04 619
619








