2015-02-04
1723
Если каждой паре чисел (x, y) из некоторой области D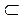 
xOy соответствует одно или несколько значений z, удовлетворяющих уравнению 
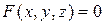, то это уравнение неявно определяет функцию 2-х переменных, например, функцию 
.
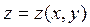Если существуют частные производные функции F (x, y, z):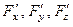 
и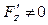 
, то существуют частные производные от функции z (x, y), которые можно вычислить по формулам:
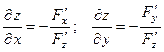. (2)
Пример. Дано: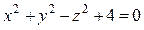 
. Найт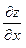и 
и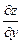 
.
Здесь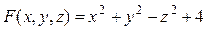 
. По формулам (2) находим:
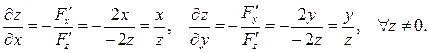
Уравнение F (x, y, z) = 0 неявно определяет еще две функции 2-х переменных: x = x (y, z) и y = y (x, z). Частные производные этих функций можно найти по формулам, аналогичным формулам (2), например:
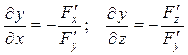. (3)
