В основе теории вероятностей лежит следующая модель: имеется комплекс условий, который можно воспроизводить в одинаковых условиях любое число раз. Каждое его воспроизведение называется опытом, испытанием или экспериментом. Предполагается, что в каждом опыте обязательно происходит одно и только одно так называемое элементарное событие (элементарный исход) 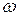 . Все множество элементарных событий, которые могут происходить в результате опыта, называется пространством элементарных событий (исходов) W[1].
. Все множество элементарных событий, которые могут происходить в результате опыта, называется пространством элементарных событий (исходов) W[1].
Случайное событие – это некоторое множество, состоящее из элементарных исходов 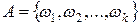 . При этом исходы
. При этом исходы 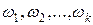 называются благоприятствующими событию
называются благоприятствующими событию 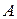 . Случайные события, так же как и множества, обычно обозначают заглавными буквами латинского алфавита с индексами или без:
. Случайные события, так же как и множества, обычно обозначают заглавными буквами латинского алфавита с индексами или без: 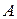 ,
, 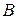 ,
, 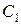 ,
, 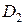 и т.д.
и т.д.
Говорят, что в результате эксперимента произошло событие 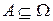 , если в эксперименте произошел один из элементарных исходов, благоприятствующих событию А.
, если в эксперименте произошел один из элементарных исходов, благоприятствующих событию А.
Достоверным называется событие, которое всегда происходит в результате рассматриваемого эксперимента. Следовательно, оно включает в себя все элементарные исходы, т.е. достоверным событием является пространство элементарных исходов 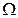 .
.
Событие называется невозможным, если оно заведомо не может произойти в результате рассматриваемого эксперимента. Значит, невозможное событие не содержит ни одного элементарного исхода, т.е. это событие является пустым множеством и обозначается 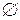 .
.
Суммой событий 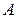 и
и 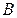 называется событие
называется событие 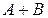 , состоящее в наступлении хотя бы одного из событий
, состоящее в наступлении хотя бы одного из событий 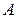 или
или 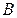 , т.е. это событие состоит из элементарных исходов, которые принадлежат либо
, т.е. это событие состоит из элементарных исходов, которые принадлежат либо 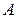 , либо
, либо 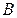 , либо двум событиям одновременно.
, либо двум событиям одновременно.
Произведением событий 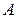 и
и 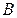 называется событие
называется событие  , состоящее в том, что оба события
, состоящее в том, что оба события 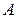 и
и 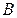 произошли одновременно, т.е. это событие состоит из элементарных исходов, принадлежащих и
произошли одновременно, т.е. это событие состоит из элементарных исходов, принадлежащих и 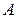 , и
, и 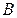 .
.
Два события 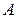 и
и 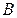 называются несовместными, если
называются несовместными, если 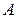 и
и 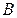 не могут произойти одновременно. Несовместные события не имеют ни одного общего благоприятствующего исхода, следовательно,
не могут произойти одновременно. Несовместные события не имеют ни одного общего благоприятствующего исхода, следовательно, 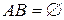 .
.
Противоположным событию 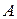 называется событие
называется событие 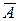 , которое происходит тогда и только тогда, когда не происходит событие
, которое происходит тогда и только тогда, когда не происходит событие 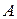 . Для противоположных событий одновременно выполняются два условия: их сумма является достоверным событием, т.е.
. Для противоположных событий одновременно выполняются два условия: их сумма является достоверным событием, т.е. 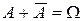 , а произведение – невозможным событием, т.е.
, а произведение – невозможным событием, т.е. 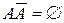 .
.
 2015-02-04
2015-02-04 614
614








