Для вычисления вероятностей сложных событий используются следующие теоремы теории вероятностей.
Теорема сложения вероятностей. Если события 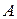 и
и 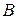 несовместны, то вероятность их суммы равна сумме их вероятностей:
несовместны, то вероятность их суммы равна сумме их вероятностей:
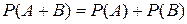 . (1)
. (1)
Сформулированная теорема справедлива для любого конечного числа слагаемых.
Если же события 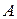 и
и 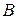 совместны, то
совместны, то
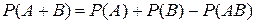 . (2)
. (2)
Из теоремы сложения вероятностей следует, что если 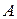 и
и 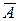 – противоположные события, то
– противоположные события, то
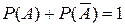 или
или 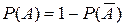 . (3)
. (3)
Теорема умножения вероятностей. Если события 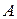 и
и 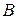 независимы (т.е. вероятность одного из событий не зависит от появления или непоявления другого), то вероятность произведения событий равна произведению их вероятностей:
независимы (т.е. вероятность одного из событий не зависит от появления или непоявления другого), то вероятность произведения событий равна произведению их вероятностей:
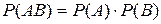 . (4)
. (4)
Сформулированная теорема также справедлива для любого конечного числа сомножителей.
Задача 2. По каналу связи передаются три сообщения. Вероятность того, что первое сообщение будет искажено равна 0,1, второе – 0,2, третье – 0,3. Найти вероятности следующих событий: 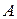 – все три сообщения переданы без искажения;
– все три сообщения переданы без искажения; 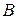 – ровно одно сообщение передано без искажения;
– ровно одно сообщение передано без искажения; 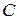 – хотя бы одно сообщение искажено.
– хотя бы одно сообщение искажено.
Решение.
Введем в рассмотрение вспомогательные события 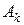 – k-ое сообщение передано без искажений,
– k-ое сообщение передано без искажений, 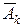 – k-ое сообщение искажено,
– k-ое сообщение искажено, 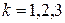 . Согласно условию
. Согласно условию 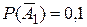 , тогда
, тогда 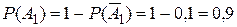 . Аналогично,
. Аналогично, 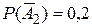 и
и 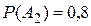 ,
, 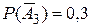 и
и 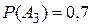 .
.
Так как событие 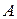 можно представить в виде
можно представить в виде 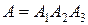 и события
и события 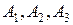 независимы, то вероятность события
независимы, то вероятность события 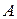 можно найти по теореме умножения вероятностей для независимых событий:
можно найти по теореме умножения вероятностей для независимых событий:
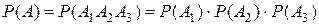
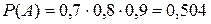 .
.
Событие 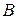 можно представить следующим образом:
можно представить следующим образом:
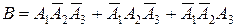 ,
,
причем слагаемые 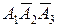 ,
, 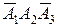 и
и 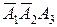 являются попарно несовместными событиями. Поэтому на основании теоремы сложения вероятностей (1) получаем:
являются попарно несовместными событиями. Поэтому на основании теоремы сложения вероятностей (1) получаем:
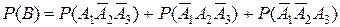 .
.
Для вычисления вероятностей событий 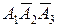 ,
, 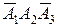 и
и 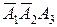 используем теорему умножения вероятностей:
используем теорему умножения вероятностей:
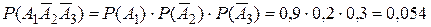 ;
;
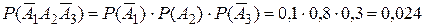 ;
;
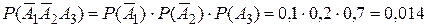 .
.
Таким образом, окончательно получаем:
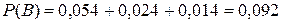 .
.
События 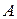 и
и 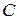 являются противоположными, следовательно,
являются противоположными, следовательно,
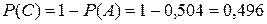 .
.
Ответы: 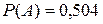 ,
, 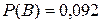 ,
, 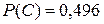 .
.
 2015-02-04
2015-02-04 965
965








