Большинство случайных величин имеют распределения, зависящие от одного или нескольких параметров. Так, например, нормальное распределение зависит от параметров 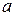 и
и 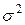 .
.
Выборочная характеристика, используемая в качестве приближенного значения неизвестного параметра генеральной совокупности, называется статистической точечной оценкой этого параметра. Статистическая оценка неизвестных параметров теоретического распределения генеральной совокупности (или просто параметров генеральной совокупности) – одна из основных задач математической статистики.
Обозначим через 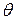 некоторый неизвестный параметр генеральной совокупности, а через
некоторый неизвестный параметр генеральной совокупности, а через 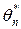 – точечную оценку этого параметра. Оценка
– точечную оценку этого параметра. Оценка 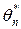 есть функция
есть функция 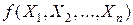 от выборки объема
от выборки объема 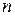 из независимых случайных величин
из независимых случайных величин 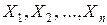 , каждая из которых имеет тот же закон распределения, что и генеральная совокупность. Поэтому оценка
, каждая из которых имеет тот же закон распределения, что и генеральная совокупность. Поэтому оценка 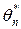 , как функция случайных величин, также является случайной величиной, в отличие от оцениваемого параметра
, как функция случайных величин, также является случайной величиной, в отличие от оцениваемого параметра 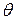 , который является величиной неслучайной, детерминированной.
, который является величиной неслучайной, детерминированной.
Оценка 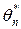 для параметра
для параметра 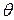 называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, т.е.
называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, т.е. 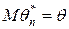 . В противном случае оценка называется смещенной.
. В противном случае оценка называется смещенной.
Несмещенность – свойство оценок при фиксированном 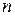 . Оно означает отсутствие ошибки "в среднем", т.е. при систематическом использовании данной оценки.
. Оно означает отсутствие ошибки "в среднем", т.е. при систематическом использовании данной оценки.
Рассмотрим некоторые наиболее часто встречающиеся точечные оценки параметров генеральной совокупности.
1. Выборочная средняя 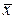 есть несмещенная оценка для генеральной средней
есть несмещенная оценка для генеральной средней 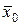 , причем
, причем 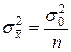 , где
, где 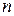 – объем выборки,
– объем выборки, 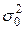 – генеральная дисперсия признака.
– генеральная дисперсия признака.
2. Выборочная дисперсия 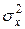 является смещенной оценкой генеральной дисперсии
является смещенной оценкой генеральной дисперсии 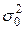 .
.
3. Исправленная дисперсия 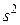 , вычисляемая по формуле
, вычисляемая по формуле
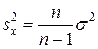 (17)
(17)
или
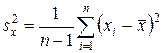 , (18)
, (18)
является несмещенной оценкой для генеральной дисперсии 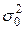 .
.
Разница между 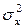 и
и 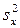 заметна при небольшом числе наблюдений
заметна при небольшом числе наблюдений 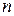 . При
. При 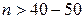 получим, что
получим, что 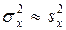 , т.е. в качестве оценки
, т.е. в качестве оценки 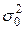 вполне можно использовать выборочную дисперсию
вполне можно использовать выборочную дисперсию 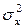 .
.
 2015-02-04
2015-02-04 569
569








