Точечные оценки параметров генеральной совокупности могут быть приняты в качестве ориентировочных, первоначальных результатов обработки выборочных данных. Их недостаток заключается в том, что неизвестно, с какой точностью оценивается параметр. Если для выборок большого объема точность обычно бывает достаточной, то для выборок небольшого объема вопрос точности оценок становится очень важным.
Чтобы получить представление о точности и надежности оценки 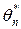 параметра
параметра 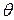 , используют интервальную оценку параметра.
, используют интервальную оценку параметра.
Интервальной оценкой параметра 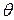 называется числовой интервал
называется числовой интервал 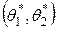 , который с заданной вероятностью
, который с заданной вероятностью 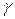 накрывает неизвестное значение параметра
накрывает неизвестное значение параметра 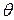 , т.е.
, т.е. 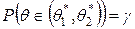 . Такой интервал
. Такой интервал 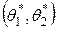 называется доверительным, а вероятность
называется доверительным, а вероятность 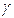 – доверительной вероятностью или надежностью оценки.
– доверительной вероятностью или надежностью оценки.
Обычно надежность оценки 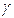 задается заранее величиной, близкой к единице, например: 0,9, 0,95, 0,99 или 0,999.
задается заранее величиной, близкой к единице, например: 0,9, 0,95, 0,99 или 0,999.
Границы доверительного интервала и его длина находятся по выборочным данным и поэтому являются случайными величинами. Длина доверительного интервала уменьшается с ростом объема выборки 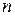 и увеличивается с ростом доверительной вероятности
и увеличивается с ростом доверительной вероятности 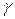 .
.
Очень часто (но не всегда) доверительный интервал выбирается симметричным относительно несмещенной точечной оценки 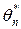 , т.е. выбирается интервал вида
, т.е. выбирается интервал вида 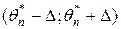 . Число
. Число 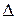 при этом называется точностью оценки.
при этом называется точностью оценки.
Так, например, интервальная оценка (доверительный интервал) для генеральной средней 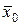 исследуемого признака
исследуемого признака 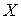 , имеющего нормальное распределение, может быть найдена по формуле:
, имеющего нормальное распределение, может быть найдена по формуле:
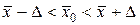 . (19)
. (19)
В случае, когда генеральная дисперсия 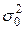 известна (например, это заранее заданная ошибка измерительного прибора), то точность оценки
известна (например, это заранее заданная ошибка измерительного прибора), то точность оценки 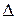 находится по формуле:
находится по формуле:
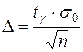 , (20)
, (20)
где 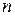 – объем выборки, а число
– объем выборки, а число 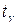 определяется из равенства
определяется из равенства 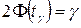 , т.е. по таблице значений функции Лапласа
, т.е. по таблице значений функции Лапласа 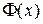 находится значение аргумента
находится значение аргумента 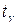 , которому соответствует значение функции
, которому соответствует значение функции 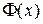 , равное
, равное 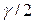 .
.
В случае, когда генеральная дисперсия 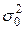 неизвестна, а известна лишь ее оценка – исправленная выборочная дисперсия
неизвестна, а известна лишь ее оценка – исправленная выборочная дисперсия 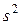 , то точность оценки
, то точность оценки 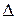 находится по формуле:
находится по формуле:
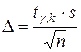 , (21)
, (21)
где значение числа 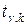 определяется по таблице критических точек распределения Стьюдента при доверительной вероятности
определяется по таблице критических точек распределения Стьюдента при доверительной вероятности 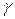 и числе степеней свободы
и числе степеней свободы 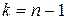 .
.
Замечание. Если выборка 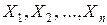 объема
объема 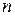 представляет собой набор независимых одинаково распределенных случайных величин, то, согласно центральной предельной теореме, распределение
представляет собой набор независимых одинаково распределенных случайных величин, то, согласно центральной предельной теореме, распределение 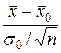 при больших
при больших 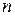 близко к стандартному нормальному. Это позволяет строить доверительный интервал для генеральной средней
близко к стандартному нормальному. Это позволяет строить доверительный интервал для генеральной средней 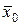 по формулам (19) и (20) при любом распределении признака, если объем выборки является достаточно большим (
по формулам (19) и (20) при любом распределении признака, если объем выборки является достаточно большим (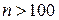 ), при этом в качестве
), при этом в качестве 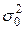 используется ее любая оценка.
используется ее любая оценка.
Задача 6. По выборке из генеральной совокупности нормально распределенного количественного признака X найти: 1) числовые характеристики выборки – выборочную среднюю, выборочную дисперсию, среднее квадратическое отклонение; 2) несмещенные оценки для генеральной средней и генеральной дисперсии; 3) доверительный интервал для оценки генеральной средней с надежностью 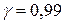 .
.
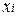
| 33,2 | 38,2 | 43,2 | 48,2 | 53,2 |
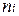
|
Решение.
1. Сначала вычислим числовые характеристики выборки.
Выборочную среднюю найдем по формуле (14).
Учитывая, что объем выборки 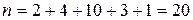 , получаем:
, получаем:
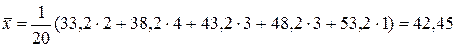 .
.
Выборочную дисперсию удобнее вычислять по формуле (16):
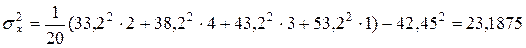 .
.
Выборочное СКО:
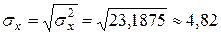 .
.
2. Несмещенной оценкой для генеральной средней 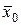 является выборочная средняя
является выборочная средняя 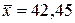 .
.
Несмещенной оценкой дисперсии 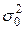 генеральной совокупности является исправленная выборочная дисперсия
генеральной совокупности является исправленная выборочная дисперсия 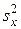 , которая вычисляется по формуле (17):
, которая вычисляется по формуле (17):
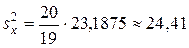 .
.
3. Так как генеральная дисперсия 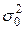 неизвестна, а известна лишь ее оценка – исправленная выборочная дисперсия
неизвестна, а известна лишь ее оценка – исправленная выборочная дисперсия 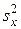 и данная выборка имеет небольшой объем (
и данная выборка имеет небольшой объем (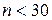 ), то доверительный интервал для генеральной средней можно найти, используя формулы (19) и (21).
), то доверительный интервал для генеральной средней можно найти, используя формулы (19) и (21).
Значение 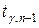 находим по таблице распределения Стьюдента, где
находим по таблице распределения Стьюдента, где 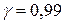 – доверительная вероятность,
– доверительная вероятность, 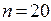 – объем выборки,
– объем выборки, 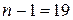 - число степеней свободы.
- число степеней свободы.
Учитывая, что 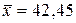 ,
, 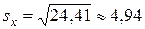 ,
, 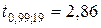 , находим сначала точность оценки по формуле (21):
, находим сначала точность оценки по формуле (21):
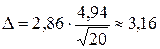 .
.
Теперь искомый доверительный интервал определяем по формуле (19):
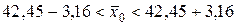
или 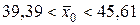 .
.
Ответы: 1. 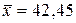 ,
, 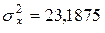 ,
, 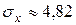 ; 2.
; 2. 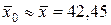 ,
, 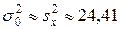 ; 3.
; 3. 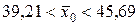 .
.
 2015-02-04
2015-02-04 664
664








