2015-02-04
562
В зависимости от вида функции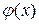 
различают линейную и нелинейную регрессию.
Для отыскания теоретического уравнения регрессии необходимо знать закон распределения двумерной случайной величины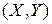 
. Но на практике исследователь располагает выборкой пар значений 
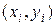ограниченного объема 
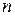. В этом случае можно построить лишь наилучшую оценку для функции регрессии, которой является выборочное уравнение регрессии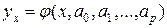 
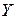на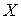 
(или просто уравнение регрессии), где 
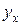– условная средняя признака 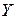при фиксированном значении признака 
, 
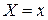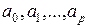– параметры уравнения регрессии.
Так, например, оценкой линейного уравнения регрессии 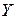на 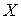является выборочное уравнение регрессии 
.
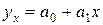Параметры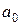 
и 
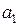выборочного уравнения регрессии находятся следующим образом:
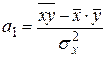; (23)
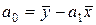, (24)
где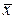 
– выборочная средняя факторного признака , 
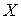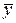– выборочная средняя результативного признака , 
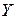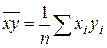– средняя из произведений соответствующих значений факторного и результативного признаков, 
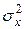– выборочная дисперсия факторного признака .
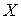Коэффициент 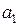в уравнении регрессии называется коэффициентом регрессии (выборочным). Он показывает, насколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.
