5178
Измерение тесноты и направления связи является важной задачей изучения и количественного измерения взаимосвязи явлений.
Если известно (или предполагается), что между результативным и факторным признаками существует линейная связь, то для оценки ее тесноты используется выборочный коэффициент корреляции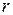 
(или просто коэффициент корреляции). Он чаще всего рассчитывается по формуле:
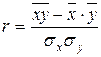. (25)
Коэффициент корреляции изменяется в пределах от –1 до +1. Равенство коэффициента нулю свидетельствует об отсутствиилинейной связи. Равенство коэффициента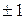 
показывает наличие функциональной связи. Знак «+» указывает напрямую связь (увеличение или уменьшение одного признака сопровождается аналогичным изменением другого признака), знак «–» – на обратную связь (увеличение или уменьшение одного признака сопровождается противоположным по направлению изменением другого признака).
В зависимости от того, насколько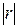 
приближается к 1, различают линейную связь слабую – 
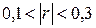, умеренную – 
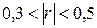, заметную – 
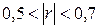, достаточно тесную – 
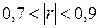и весьма тесную – 
.
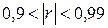В отличие от коэффициента регрессии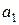 
коэффициент корреляции 
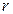не зависит от принятых единиц измерения признаков, а, следовательно, он сравним для любых признаков.
Как любая статистическая величина, коэффициент корреляции подвержен случайным колебаниям в результате выборочности исследования.
Для оценки значимости коэффициента корреляции применяется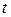 
-критерий Стьюдента. При этом определяется эмпирическое значение критерия 
:
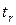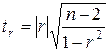. (26)
Вычисленное по формуле (27) значение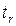 
сравнивается с критическим, которое берется из таблицы значений 
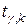распределения Стьюдента с учетом заданного уровня значимости 
( 
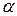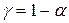) и числа степеней свободы 
.
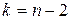Если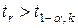 
, то величина коэффициента корреляции признается значимой.
Задача 8. Имеются следующие данные об уровне механизации работ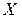 
(%) и производительности труда 
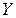(т/чел.) для 14 однотипных предприятий:
| № п/п | |||||||
| |||||||
|
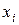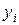| № п/п | |||||||
|
| |||||||
|
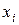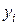Требуется: 1) оценить тесноту и направление связи между признаками с помощью коэффициента корреляции и оценить значимость коэффициента корреляции на уровне значимости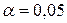 
; 2) найти уравнение линейной регрессии 
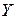на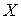 
; 3) в одной системе координат построить эмпирическую и теоретическую линии регрессии.
Решение.
1. Для удобства проведем все необходимые предварительные расчеты в таблице.
Таблица 1
Расчетная таблица
| № п/п |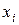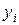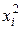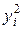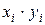
|
| 
| 
| 
|
| Всего |
Рассчитаем числовые характеристики выборки, используя итоговую строку расчетной таблицы и учитывая, что объем выборки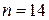 
:
· выборочные средние:
;
;
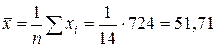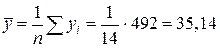· средние по квадратам:
;
;
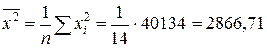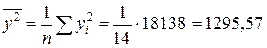· средняя по произведениям:
;
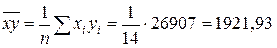· выборочные средние квадратические отклонения:
; 
;
; 
.
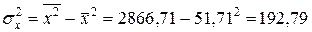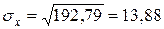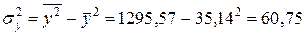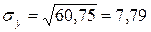Вычислим выборочный коэффициент корреляции по формуле (26):
.
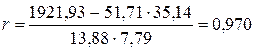Т.к.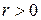 
и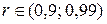 
, то, следовательно, линейная связь между изучаемыми признаками является прямой и весьма тесной.
Оценим значимость выборочного коэффициента корреляции. Для этого рассчитаем эмпирическое значение 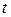-критерия по формуле (26):
.
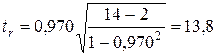Для уровня значимости 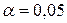и числа степеней свободы 
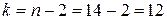находим критическое значение 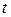-критерия: 
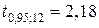по таблице значений 
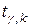распределения Стьюдента. Поскольку 
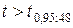, то коэффициент корреляции между признакам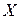и 
и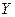 
является значимым (или значимо отличается от нуля).
2. Найдем уравнение линейной регрессии 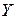на :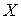 
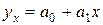, вычислив параметры уравнения регрессии по формулам (23) и (24):
;
.
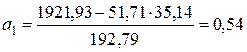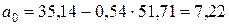Следовательно, уравнение прямой регрессии имеет вид:
.
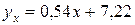3) Построим в одной системе координат эмпирическую и теоретическую линии регрессии. Эмпирическая линия – это ломаная, соединяющая точки с координатами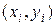 
, а теоретическая – это график прямой регрессии, уравнение которой было получено в п. 2. Теоретическую линию регрессии можно построить по двум точкам, абсциссы которых выбираются произвольно, а ординаты находятся по построенному уравнению регрессии. Найдем координаты точек для построения теоретической линии регрессии: 
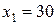, тогда 
; 
, 
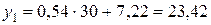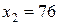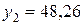. Значит, теоретическую линию регрессии будем строить по двум точкам с координатам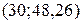и 
и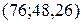 
.
|
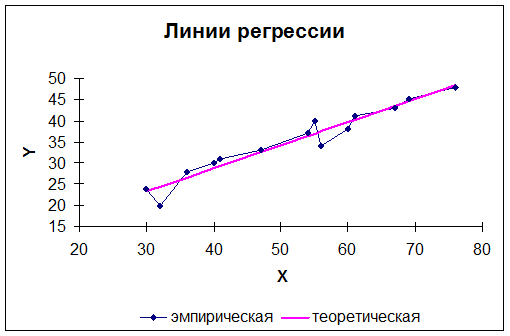| Рис. 2. Эмпирическая и теоретическая линии регрессии |
Ответ: 1)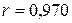 
, линейная связь прямая, весьма тесная, коэффициент корреляции значим на уровне значимости 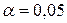; 2) выборочное уравнение прямой регрессии 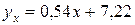; 3) линии регрессии представлены на рис. 2.
