Задание. 1. Построить линейное уравнение парной регрессии у от х

1. Построить линейное уравнение парной регрессии у от х.

2. Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.

3. Оценить статистическую значимость параметров регрессии и корреляции.

4. Построить доверительный интервал для коэффициента регрессии с вероятностью 95%.

Решение. Для расчета параметров уравнения линейной регрессии строим расчетную таблицу 2.

Таблица 2

№	y	x	xy	x2	y2	yx	|y-yx|	|(y-yx)/y|
		39,0						0,119
		41,0						0,030
		43,5						0,172
		39,5						0,028
		44,5						0,019
		53,0						0,105
		33,5						0,003
		44,0						0,000
		36,5						0,052
		43,5						0,031
		38,0						0,076
		57,5						0,057
Итого (в среднем)		42,8					x	0,690

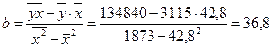
a= `y – b *`x = 3115-36,8*42,8 = 1539,5

Отсюда уравнение регрессии имеет вид: у_х=1539,5+36,8х.

С увеличением расхода кормов на корову на 1 ц. корм.ед. среднегодовой надой на 1 корову в среднем возрастает на 36,8 кг. Тесноту линейной связи оценим с помощью коэффициента корреляции. Для этого сначала найдем среднеквадратические отклонения х и у по формулам:

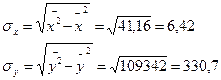
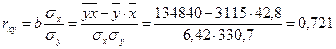
Коэффициент корреляции показывает, что связь между х и у характеризуется как сильная. Определим качество модели через среднюю ошибку аппроксимации: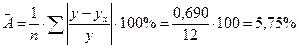

Качество модели можно оценить как хорошее, так как `А не превышает 8-10%. Коэффициент детерминации r² равен 0,52. Это означает, что 52% вариации уровня удоев молока от одной коровы объясняется вариацией фактора х – расход кормов на корову.

Оценим значимость уравнения в целом с помощью F-критерия:

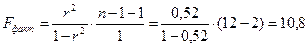
Определим критическое значения критерия по таблице (см. приложение) при к₁=1, к₂=10 и уровне значимости a=0,05. Оно равно 4,96. Так как F_факт > F_кр, то гипотезу Н₀ о случайном характере связи отклоняем с вероятностью 95%. Уравнение регрессии статистически значимо.

Оценку статистической значимости параметров регрессии прове­дем с помощью t-статистики Стьюдента. Выдвигаем гипотезы H₀ о статистически незначимом отличии показателей от нуля: а=b=r=0. Табличное t_кр для числа степеней свободы df= n-2=12-2=10 и a= 0,05 составит 2,23.

Определим случайные ошибки m_b, m_a, m_r:

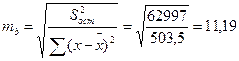
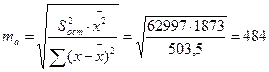
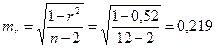
Тогда t_b=36,8/11,19=3,29, t_a=1539,5/484=3,18, t_r=0,721/0,219=3,29. Фактические значения t-статистики превосходят табличные значе­ния:

t_b =3,29 > t_кр=2,23, t_a =3,18 > t_кр=2,23, t_r =3,29 > t_кр=2,23.

Поэтому гипотезы Н₀ отклоняется, т.е. а,b и r не случайно отлича­ются от нуля, а статистически значимы с вероятностью 95%. Зная связь между F и t-критериями можно было найти t-критерий для b и r по-другому:

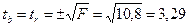
Результаты проверки надежности отдельных параметров согласуются с результатами проверки уравнения в целом. Рассчитаем доверительный интервал для коэффициента регрессии b. Для этого определим предельную ошибку D=t_кр*m_b=2,23*11,19=25,0. Соответственно доверительный интервал при 5% уровне значимости будет:

36,8-25,0£ b £36,8+25,0

11,8£ b £61,8

Анализ верхней и нижней границ доверительного интервала приводит к выводу о том, что с вероятностью р =1-a=0,95 коэффициент регрессии b, находясь в указанных границах, не принимает нулевого значения, т.е. не являются статистически незначимым и сущест­венно отличен от нуля.

Кроме этого применяются характеристики множественной регрессии и корреляции. Основными уравнениями являются линейные уравнения множественной регрессии в стандартизованной и естественной формах. Уравнение в естественной форме y=a+b₁x₁+b₂x₂+…+b_nx_n оценивается МНК:

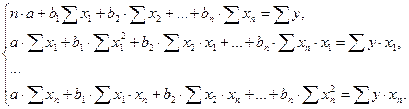(7)

Нахождение параметров уравнение регрессии в стандартизированном масштабе t_y=b₁t_x1+b₂t_x2+…+b_pt_xp осуществляется через коэффициенты парной корреляции:

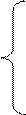r_yx1=b₁+b₂r_x2x1+…+b_pr_xpx1,

r_yx2=b₁r_x1x2 +b₂+…+b_pr_xpx2, (8)

_…

r_yxp=b₁r_x1xp +b₂r_x2xp+…+b_p.

Существует связь между b- и b-коэффициентами: 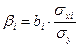(9)

При трех переменных для двухфакторного уравнения регрес­сии формула совокупного коэффициента корреляции R_yx1x2 приводима к следующему виду:

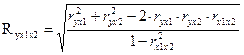(10)

При линейной зависимости признаков формула индекса кор­реляции может быть получена через стандартизированные коэффициенты:

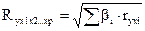(11)

Оценка качества построенной модели проводится аналогично парной регрессии и корреляции. Во множественной регрессии появляется еще один F-критерий - частный, определяющий целесообразность включения отдельного фактора после всех остальных:

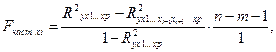(12)

где R²_x1…xp – индекс множественной детерминации для модели с полным набором факторов;

R²_{x1…xi-1,xi+1…xp} – индекс множественной детерминации, но без включения в модель фактора х_i.

Фактическое значение частного F-критерия сравнивается с критическим (табличным) при 5%- или 1%-ом уровне значимости и числе степеней свободы: k₁=1 и k₂=n-m-1.

Частные коэффициенты (или индексы) корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии. При двух факторах показатели частной корреляции примут вид:

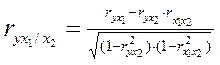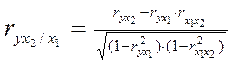и (13)

Пример 2. По 30 наблюдениям матрица парных коэффициентов корреляции оказалась следующей:

	у	x1	х2	х3
у x1 х2 х3	1,00 0,30 0,60 0,40	1,00 0,10 0,15	1,00 0,80	1,00