Электрон в потенциальной яме

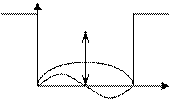
Рассмотрим движение микрочастицы энергии E в прямоугольной потенциальной яме (рис. 2.2) глубиной U ₀ и шириной L.

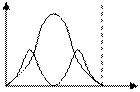U w

U ₀ E II

I III

0 L x 0 L x

a) б)

Рис. 2.2. Частица в потенциальной яме: а – энергетическая диаграмма; б – вероятность нахождения частицы

Для электрона примером такой ямы является микроэлектрод: вне электрода энергия электрона равняется нулю, а внутри – U ₀. Эта энергия обеспечивается потенциальным полем решетки U ₀. Для выхода электрона из металла необходимо совершить работу, равную U ₀ – работу выхода.

Запишем стационарное уравнение Шредингера для областей I, II, и III (рис. 2.2, а).

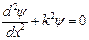, (2.28)

где ,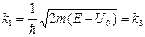

.

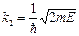Запишем общее решение уравнения Шредингера для трех зон.

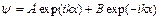, (2.29)

Упростим задачу, считая, что U ₀"∞. Тогда в областях I и III волновая функция будет равна нулю.

Согласно условию непрерывности функции можно записать, что

ψ (0)= ψ (L)=0. (2.30)

Это условие выполнимо, если

kL = πn, n = 1, 2, …

Отсюда находим возможные значения k_n

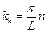. (2.31)

Поскольку стенки ямы имеют одинаковую высоту, очевидно, что в (2.29) A = B. Тогда можно записать выражение для волновой функции электрона в яме

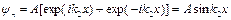
или

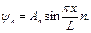(2.32)

В потенциальной яме укладывается целое число полуволн (рис. 2.2, б). Определим вероятность нахождения электрона в потенциальной яме ω (x).

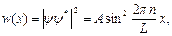
где А – коэффициент, определяемый из условия нормировки, .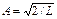

Тогда можно записать

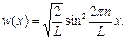(2.33)

Из данного выражения следует, что в отличие от свободного электрона вероятность нахождения электрона в потенциальной яме непостоянна и изменяется с изменением квантового числа n (рис. 2.2, б).

Вернемся к выражению (2.28) и запишем выражение для энергии электрона в яме.

.

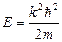Полученное выражение не отличается от записанного ранее (2.22) для свободного электрона. Однако, подставив в него k из (2.31), получим новое выражение

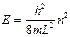. (2.34)

Полученное выражение содержит квантовое число n, т.е. спектр энергии электрона в потенциальной яме является не сплошным, как для свободного электрона, а дискретным.