Уравнение Шредингера. Волновая функция

Из вышеизложенного с очевидностью следует, что в микромире классическая механика неприменима. Ее место занимает квантовая механика – раздел теоретической физики, описывающий поведение микрочастиц.

Аналогом основного уравнения динамики для микромира является уравнение, постулированное Шредингером и носящее его имя. Для микрочастицы, находящейся в силовом поле и обладающей потенциальной энергией U (x, y, z, t), уравнение имеет следующий вид:

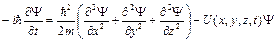, (2.7)

где Ψ – волновая функция, в общем случае зависящая от координат и времени;

i – мнимая единица.

Волновая функция описывает поведение микрочастицы. Она является комплексной функцией, и физический смысл имеет не сама функция, а ее произведение на комплексно сопряженную функцию Ψ ^*. Такое произведение действительно и пропорционально вероятности того, что в момент t частица находится в элементе объема dV. Эта вероятность ω (x, y, z, t) определяется из выражения

w (x, y, z, t) dV = Ψ(x, y, z, t) Ψ ^* (x, y, z, t) dV. (2.8)

В соответствии со смыслом волновой функции, она должна быть непрерывной, однозначной и конечной во всех точках пространства, а также иметь непрерывную первую производную.

Для волновой функции справедливо условие нормировки

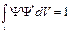, (2.9)

которое свидетельствует, что нахождение частицы в объеме V, если она находится в элементе этого объема, событие достоверное.

В общем случае потенциальная энергия микрочастицы зависит от координат и времени. Однако существует ряд задач для полей стационарного характера. В этих практически важных случаях потенциальная энергия не зависит от времени. Тогда выражение для волновой функции можно представить в виде произведения

Ψ(x, y, z, t) = ψ (x, y, z) φ (t). (2.10)

Для простоты выберем одномерный случай. Тогда можно записать

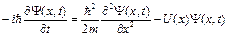, (2.11)

Ψ(x, t) = ψ (x) φ (t). (2.12)

Подставив (2.12) в (2.11) и разделив переменные, получим

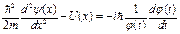, (2.13)

Левая часть равенства является функцией только x, правая часть зависит только от t. Это возможно только тогда, когда каждая часть равна одной и той же постоянной величине. Можно показать, что эта постоянная есть полная энергия частицы E. Приравняем левую и правую части к E и преобразуем их. Тогда получим два уравнения для одномерного стационарного случая

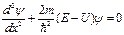, (2.14)

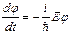. (2.15)

Последнее уравнение легко интегрируется и дает решение в виде

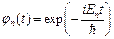, (2.16)

где E_n – одно из собственных значений энергии частицы.

Из формулы (2.16) видно, что функция φ_n (t) является гармонической с частотой ν_n = E_n / ћ.

Для того чтобы решить уравнение (2.14), необходимо определить вид функции потенциального поля U (x) и подставить его в (2.14). Тогда решение (2.13) будет иметь вид

Ψ(x, t)=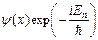. (2.17)