Если в системе действуют диссипативные силы (силы трения), колебания становятся затухающими. По второму закону Ньютона имеем
max=Fупр+Fтр (11)
где Fтр – сила трения равная
Fтр=r 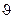 (12)
(12)
где r – коэффициент сопротивления среды,
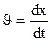 – скорость колеблющегося тела.
– скорость колеблющегося тела.
Дифференциальное уравнение незатухающих колебаний записывается в виде
max+ 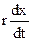 +kx=0 (13)
+kx=0 (13)
Это уравнение можно преобразовать, разделив почленно на m
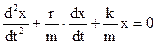 (14)
(14)
дифференциальное уравнение затухающих гармонических колебаний.
Обозначим 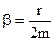 - называемый коэффициент затухания.
- называемый коэффициент затухания.
Решение дифференциального уравнения (закон затухающих колебаний) имеет вид
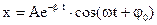 (15)
(15)
где 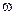 - циклическая частота затухающих колебаний, связанная с частотой незатухающих колебаний и зависящая от свойств внешней среды.
- циклическая частота затухающих колебаний, связанная с частотой незатухающих колебаний и зависящая от свойств внешней среды.
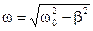 (16)
(16)
Ввиду затухания такие колебания не являются строго периодическими. Под их периодом понимают интервал времени между двумя последовательными максимальными отклонениями от положения равновесия.
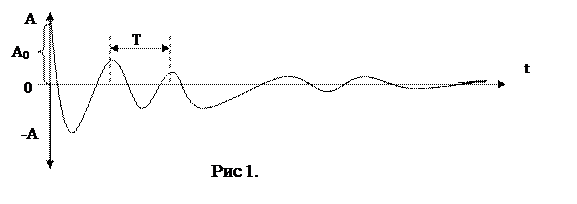 |
Амплитуда таких колебаний с течением времени убывает по экспоненциальному закону
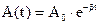 (17)
(17)
где А0 – начальная амплитуда,
е – основание натурального логарифма.
Быстроту затухания колебаний характеризуют физической величиной, называемой логарифмическим декрементом затухания 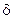 , численно равен натуральному логарифму отношения амплитуд, отстоящих друг от друга по времени на период колебаний.
, численно равен натуральному логарифму отношения амплитуд, отстоящих друг от друга по времени на период колебаний.
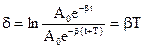 (18)
(18)
 2015-02-04
2015-02-04 327
327








