Имитационное моделирование

Имитационное моделирование является мощным инструментом исследования поведения реальных систем. Методы имитационного моделирования позволяют собрать необходимую информацию о поведении системы путем создания ее компьютерной модели. Эта информация используется затем для проектирования системы.

Цель имитационного моделирования состоит в воспроизведении поведения исследуемой системы на основе результатов анализа наиболее существенных взаимосвязей между ее элементами в предметной области для проведения различных экспериментов.

Имитационное моделирование позволяет имитировать поведение системы во времени. Причём плюсом является то, что временем в модели можно управлять: замедлять в случае с быстропротекающими процессами и ускорять для моделирования систем с медленной изменчивостью. Можно имитировать поведение тех объектов, реальные эксперименты с которыми дороги, невозможны или опасны.

К имитационному моделированию прибегают, когда:

1. Дорого или невозможно экспериментировать на реальном объекте.

2. Невозможно построить аналитическую модель: в системе есть время, причинные связи, последствие, нелинейности, стохастические (случайные) переменные.

3. Необходимо сымитировать поведение системы во времени.

Имитация, как метод решения нетривиальных задач, получила начальное развитие в связи с созданием ЭВМ в 1950х — 1960х годах.

Можно выделить две разновидности имитации:

1. Метод Монте-Карло (метод статистических испытаний);

2. Метод имитационного моделирования (статистическое моделирование).

В настоящее время выделяют три направления имитационных моделей:

1. Агентное моделирование — относительно новое (1990е-2000е гг.) направление в имитационном моделировании, которое используется для исследования децентрализованных систем, динамика функционирования которых определяется не глобальными правилами и законами (как в других парадигмах моделирования), а наоборот. Когда эти глобальные правила и законы являются результатом индивидуальной активности членов группы.

Цель агентных моделей — получить представление об этих глобальных правилах, общем поведении системы, исходя из предположений об индивидуальном, частном поведении ее отдельных активных объектов и взаимодействии этих объектов в системе. Агент — некая сущность, обладающая активностью, автономным поведением, может принимать решения в соответствии с некоторым набором правил, взаимодействовать с окружением, а также самостоятельно изменяться.

2. Дискретно-событийное моделирование — подход к моделированию, предлагающий абстрагироваться от непрерывной природы событий и рассматривать только основные события моделируемой системы, такие как: «ожидание», «обработка заказа», «движение с грузом», «разгрузка» и другие. Дискретно-событийное моделирование наиболее развито и имеет огромную сферу приложений — от логистики и систем массового обслуживания до транспортных и производственных систем. Этот вид моделирования наиболее подходит для моделирования производственных процессов.

3. Системная динамика — парадигма моделирования, где для исследуемой системы строятся графические диаграммы причинных связей и глобальных влияний одних параметров на другие во времени, а затем созданная на основе этих диаграмм модель имитируется на компьютере. По сути, такой вид моделирования более всех других парадигм помогает понять суть происходящего выявления причинно-следственных связей между объектами и явлениями. С помощью системной динамики строят модели бизнес-процессов, развития города, модели производства, динамики популяции, экологии и развития эпидемии.

Основные понятия построения модели

Имитационное моделирование основано на воспроизведении с помощью компьютеров развернутого во времени процесса функционирования системы с учетом взаимодействия с внешней средой.

Основой всякой имитационной модели (ИМ) является:

· разработка модели исследуемой системы на основе частных имитационных моделей (модулей) подсистем, объединенных своими взаимодействиями в единое целое;

· выбор информативных (интегративных) характеристик объекта, способов их получения и анализа;

· построение модели воздействия внешней среды на систему в виде совокупности имитационных моделей внешних воздействующих факторов;

· выбор способа исследования имитационной модели в соответствии с методами планирования имитационных экспериментов (ИЭ).

Условно имитационную модель можно представить в виде действующих, программно (или аппаратно) реализованных блоков.

На рисунке показана структура имитационной модели. Блок имитации внешних воздействий (БИВВ) формирует реализации случайных или детерминированных процессов, имитирующих воздействия внешней среды на объект. Блок обработки результатов (БОР) предназначен для получения информативных характеристик исследуемого объекта. Необходимая для этого информация поступает из блока математической модели объекта (БМО). Блок управления (БУИМ) реализует способ исследования имитационной модели, основное его назначение – автоматизация процесса проведения ИЭ.

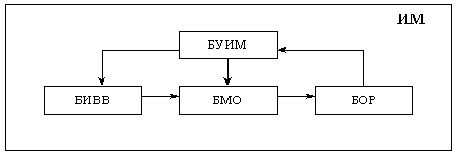
Целью имитационного моделирования является конструирование ИМ объекта и проведение ИЭ над ней для изучения закономерностей функционирования и поведения с учетом заданных ограничений и целевых функций в условиях имитации и взаимодействия с внешней средой.

Принципы и методы построения имитационных моделей

Процесс функционирования сложной системы можно рассматривать как смену ее состояний, описываемых ее фазовыми переменными

Z1(t), Z2(t), Zn(t) в n – мерном пространстве.

Задачей имитационного моделирования является получение траектории движения рассматриваемой системы в n – мерном пространстве (Z1, Z2, Zn), а также вычисление некоторых показателей, зависящих от выходных сигналов системы и характеризующих ее свойства.

В данном случае “движение” системы понимается в общем смысле – как любое изменение, происходящее в ней.

Известны два принципа построения модели процесса функционирования систем:

1. Принцип Δt для детерминированных систем

Предположим, что начальное состояние системы соответствует значениям Z1(t0), Z2(t0), Zn(t0). Принцип Δt предполагает преобразование модели системы к такому виду, чтобы значения Z1, Z2, Zn в момент времени t1 = t0 + Δt можно было вычислить через начальные значения, а в момент t2 = t1+ Δt через значения на предшествующем шаге и так для каждого i-ого шага (t = const, i = 1 M).

Для систем, где случайность является определяющим фактором, принцип Δt заключается в следующем:

1. Определяется условное распределение вероятности на первом шаге (t1 = t0+ Δt) для случайного вектора, обозначим его (Z1, Z2, Zn). Условие состоит в том, что начальное состояние системы соответствует точке траектории.

2. Вычисляются значения координат точки траектории движения системы (t1 = t0+ Δt), как значения координат случайного вектора, заданного распределением, найденным на предыдущем шаге.

3. Отыскиваются условное распределение вектора на втором шаге (t2 = t1 + Δ t), при условии получения соответствующих значений на первом шаге и т.д., пока ti = t0 + i Δ t не примет значения (tМ = t0 + М Δ t).

Принцип Δ t является универсальным, применим для широкого класса систем. Его недостатком является неэкономичность с точки зрения затрат машинного времени.

2. Принцип особых состояний (принцип δz).

При рассмотрении некоторых видов систем можно выделить два вида состояний δz:

1. Обычное, в котором система находится большую часть времени, при этом Zi(t), (i=1 n) изменяются плавно;

2. Особое, характерное для системы в некоторые моменты времени, причем состояние системы изменяется в эти моменты скачком.

Принцип особых состояний отличается от принципа Δt тем, что шаги по времени в этом случае не постоянны, является величиной случайной и вычисляется в соответствии с информацией о предыдущем особом состоянии.

Примерами систем, имеющих особые состояния, являются системы массового обслуживания. Особые состояния появляются в моменты поступления заявок, в моменты освобождения каналов и т.д.

Основные методы имитационного моделирования.

Основными методами имитационного моделирования являются: аналитический метод, метод статического моделирования и комбинированный метод (аналитико-статистический) метод.

Аналитический метод применяется для имитации процессов в основном для малых и простых систем, где отсутствует фактор случайности. Метод назван условно, так как он объединяет возможности имитации процесса, модель которого получена в виде аналитически замкнутого решения, или решения полученного методами вычислительной математики.

Метод статистического моделирования первоначально развивался как метод статистических испытаний (Монте-Карло). Это – численный метод, состоящий в получении оценок вероятностных характеристик, совпадающих с решением аналитических задач (например, с решением уравнений и вычислением определенного интеграла). В последствии этот метод стал применяться для имитации процессов, происходящих в системах, внутри которых есть источник случайности или которые подвержены случайным воздействиям. Он получил название метода статистического моделирования.

Комбинированный метод (аналитико-статистический) позволяет объединить достоинства аналитического и статистического методов моделирования. Он применяется в случае разработки модели, состоящей из различных модулей, представляющих набор как статистических так и аналитических моделей, которые взаимодействуют как единое целое. Причем в набор модулей могут входить не только модули соответствующие динамическим моделям, но и модули соответствующие статическим математическим моделям.

Вопросы для самопроверки

1. Определить, что такое оптимизационная математическую модель.

2. Для чего могут использоваться оптимизационные модели?

3. Определить особенности имитационного моделирования.

4. Дать характеристику метода статистического моделирования.

5. Что есть модель типа «черный ящик», модель состава, структуры, модель типа «белый ящик»?