2015-02-04
1553
1) создадим лист «Корреляция вручную». Скопируем случайные величины Х1, Х2, Х3, Y на созданный лист (для удобства их можно закрасить).
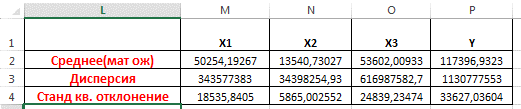
2) рассчитаем среднее (мат. ожидание), дисперсию, среднеквадратическое отклонение для каждой случайной величины, используя стандартные функции MS Excel, например как представлено на рис. 33.
| Рис. 33 Расчет математического ожидания, дисперсии, среднеквадратического отклонения для каждой случайной величины |
3) для удобства дальнейших расчетов корреляционного момента добавим новые столбцы справа каждой случайной величины как показано на рис. 34 и найдем следующие произведения разностей: (x1i-mx1)*(x2i-mx2); (x1i-mx1)*(x3i-mx3); (x1i-mx1)*(yi-mxy); (x2i-mx2)*(x3i-mx3); (x2-mx2)*(y-mxy); (x3-mx3)*(y-mxy). (рис. 34).
| Рис. 34 Произведения разностей |
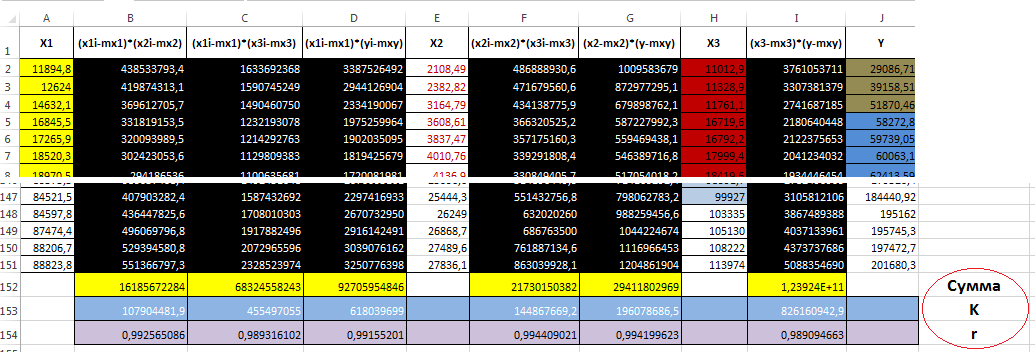
После того как нашли все произведения, рассчитываем сумму для каждого столбца и разделив ее на число опытов n=150 найдем корреляционные моменты для сочетаний (Х1,Х2);(Х1,Х3);(Х1,У);(Х2,Х3);(X2,Y);(X3,Y) см. рис. 34.
Разделив значения корреляционного момента для каждого сочетания на произведение их среднеквадратических отклонений, соответственно получим корреляционные моменты для каждого сочетания. Далее по формуле (1) рассчитаем коэффициент корреляции. (рис. 34).
