Примем за первое ведущее уравнение первое уравнение системы, а за первое ведущее неизвестное – x 1; первым ведущим элементом будет a 11 = 2. Исключим x 1 из второго и третьего уравнений, прибавив ко второму уравнению ведущее, умноженное на 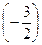 , а к третьему – ведущее, умноженное на
, а к третьему – ведущее, умноженное на 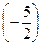 .
.
Получим:
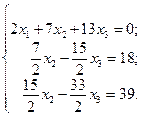
Первый шаг закончен. Второе и третье уравнения образуют первую подсистему. За второе ведущее уравнение примем второе уравнение системы, а за второе ведущее неизвестное x 2; вторым ведущим элементом будет 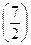 . Исключим x 2 из третьего уравнения, прибавив к третьему ведущее, умноженное на
. Исключим x 2 из третьего уравнения, прибавив к третьему ведущее, умноженное на 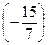 .
.
Получим:
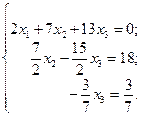
Второй шаг закончен. Вторая подсистема состоит из одного третьего уравнения. Прямой ход метода Гаусса закончен. Обратным ходом получаем:
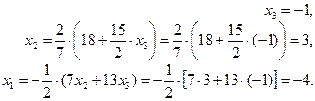
Итак, решение данной системы будет: x 1 = –4, x 2 = 3, x 3 = –1.
Задача
Решить систему уравнений методом главных элементов с точностью ε < 0.001.
Варианты
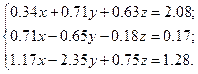
| 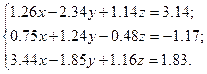
| ||
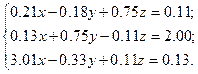
| 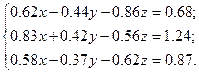
| ||
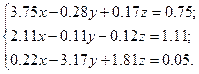
| 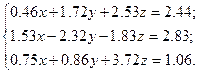
| ||
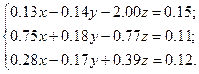
| 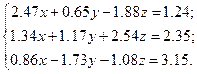
| ||
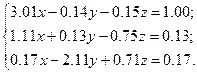
| 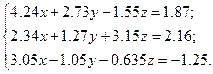
| ||
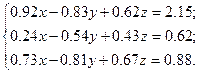
| 
| ||
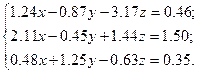
| 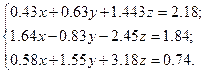
| ||
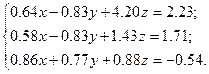
| 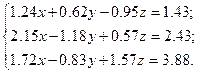
| ||
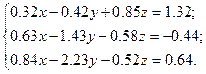
| 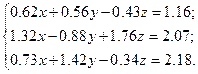
| ||
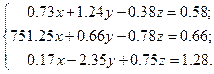
| 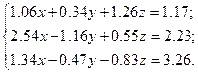
|
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 4. Ознакомление счисленными методами интегрирования (3 ч)
Цель работы – дать студенту возможность изучить алгоритмы и методы вычисления определённых интегралов.
Теоретические сведения.
Многие инженерные задачи, задачи физики, геометрии и многих других областей человеческой деятельности приводят к необходимости вычислять определённый интеграл вида
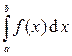 ,
,
где f (x) – подынтегральная функция, непрерывная на отрезке [ a; b ].
Непрерывность функции является достаточным условием её интегрируемости. Однако определённый интеграл может существовать и для некоторых разрывных функций, в частности для всякой ограниченной функции, имеющей на нём конечное число точек разрыва.
Определённый интеграл однозначно связан с неопределённым интегралом, или первообразной, формулой Ньютона – Лейбница
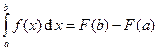 . (15.1)
. (15.1)
где F (b) и F (a) – любая первообразная функции f (x), вычисленная в точках b и a соответственно.
Если же интеграл от данной функции не может быть вычислен по формуле (15.1), т. е. не выражается через элементарные функции, или если функция f (x) задана графически или таблицей, то для вычисления определённого интеграла применяют приближённые формулы. Для приближённого вычисления интеграла (15.1) существует много численных методов, таких как:
• метод прямоугольников;
• трапеций;
• Симпсона и др.
Примеры интегралов, имеющих большое значение в приложениях, но не выражающихся через элементарные функции:
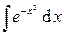 – интеграл Пуассона (теория вероятностей),
– интеграл Пуассона (теория вероятностей),
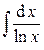 – интегральный логарифм (теория чисел),
– интегральный логарифм (теория чисел),
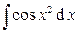 ,
, 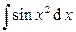 – интегралы Френеля (физика),
– интегралы Френеля (физика),
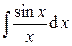 ,
, 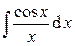 – интегральные синус и косинус,
– интегральные синус и косинус,
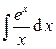 – интегральная показательная функция.
– интегральная показательная функция.
При вычислении интеграла следует помнить, каков геометрический смысл определённого интеграла.
Если f (х) ≥ 0 на отрезке [ a; b ], то 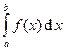 численно равен площади фигуры, ограниченной графиком функции y = f (x), отрезком оси абсцисс, прямой x = a и прямой x = b (рисунок 15.1). Таким образом, вычисление интеграла равносильно вычислению площади S криволинейной трапеции.
численно равен площади фигуры, ограниченной графиком функции y = f (x), отрезком оси абсцисс, прямой x = a и прямой x = b (рисунок 15.1). Таким образом, вычисление интеграла равносильно вычислению площади S криволинейной трапеции.
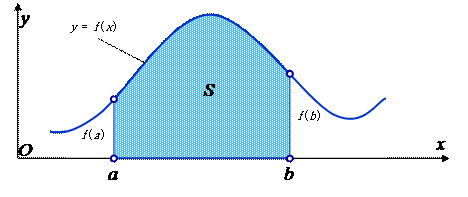 |
Рисунок 13 – Геометрический смысл определённого интеграла
 2015-02-04
2015-02-04 537
537








