Простейшим входным сигналом, используемым при идентификации, является ступенчатый сигнал. Такой сигнал на входе системы может быть сформирован, например, путем внезапного открывания (или закрывания) входного клапана, включения (или выключения) управляющего напряжения или тока и т.д., так как это почти всегда возможно без применения специальной аппаратуры. У идеального ступенчатого сигнала время нарастания сигнала равно нулю, что физически невозможно, так как при этом скорость нарастания должна быть бесконечно большой. Следовательно, любой реальный ступенчатый входной сигнал является лишь аппроксимацией идеального ступенчатого сигнала. Однако, если время нарастания сигнала гораздо меньше периода высшей гармоники, то ошибка идентификации становится незначительной. В процессах с помехами или в случаях, когда измерения содержат шум (что обычно имеет место на практике), необходима соответствующая фильтрация шума.
Идентификация с помощью переходной функции проводится автономно, вне процесса управления, и поэтому применима только к стационарным процессам. Однако, поскольку ступенчатые возмущения воздействуют на многие системы во время включения или в процессе нормальной работы, то переходные функции можно записать, не нарушая нормального режима работы системы. В этом заключается дополнительное преимущество рассматриваемого метода. Очевидно, что при этом необходимо предположить, что система стационарная, так как результаты идентификации считаются достоверными и после приложения ступенчатого сигнала. Кроме того, предполагается, что в диапазоне амплитуд ступенчатого сигнала система линейна.
Во многих случаях для определения передаточной функции системы можно использовать запись ее переходной функции. Такой способ применим к большинству типов линейных систем (1 и 2 порядков и к апериодическим системам высшего порядка). Наиболее корректно графический метод идентификации с использованием переходных функций применяется к процессам первого порядка.
Дан график переходного процесса. В момент времени t0=0 входная величина x скачком изменяется на величину a. Надо записать уравнение объекта. Искомое уравнение для объекта первого порядка имеет вид
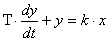 или
или 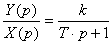 .
.
Надо определить параметры уравнения T и k.
Рассмотрим несколько методов определения этих параметров:
а) вначале найдем аналитическое решение уравнения при заданных начальных условиях. В это решение войдут T и k. Сравнивая графическое и аналитическое решения. получим параметры аналитического выражения решения. Для начальных условий: y=0 при t=0 иx=a при t>0, общее выражение для решения этого уравнения запишется в следующем виде:
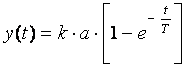 .
.
Возьмем на графике две точки (этого достаточно). Подставив координаты этих точек в выражение решения, получим два уравнения для определения двух неизвестных T и k
 .
.
Однако эти уравнения трансцендентные, поэтому вычислить из них T и k очень трудно. К тому же точность решения мала, так как использовались только две точки графика;
б) для получения более точного решения, разделим график на ординаты y1, y2, y3,… с шагом ∆t. Используя общее решение, для полученных точек можно записать:

и так далее. Имеем
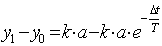 ,
,  ,
, 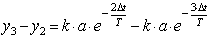 и т.д.
и т.д.
Обозначим 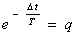 , тогда
, тогда
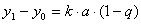 ,
, 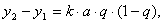
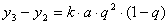 и т.д.
и т.д.
Имеем
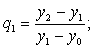
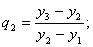
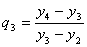 и т.д.
и т.д.
Разница в значениях q обусловлена ошибками эксперимента и определения значений y(t). Вычислив среднее арифметическое 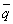 полученных значений qi, можем получить уточненное значение постоянной времени из следующего выражения:
полученных значений qi, можем получить уточненное значение постоянной времени из следующего выражения: 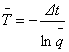 (из
(из 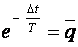 ,
, 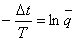 ).
).
Аналогично, вычислив
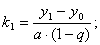
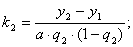
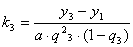 и т.д.,
и т.д.,
определяем уточненное среднее значение 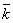 ;
;
в) на практике чаще используется следующий более простой метод.
При t, стремящемся к ∞ имеем y(t) = k*a, то есть через ординату асимптоты (ордината асимптоты b=ka) можно определить k. Коэффициент k представляет собой соотношение между установившейся величиной выходного сигнала системы и амплитудой входного сигнала.
При t = T функция
y (t)=b· 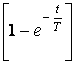 = b· (1-e-1) = b· (1-0.37) = 0.63·b.
= b· (1-e-1) = b· (1-0.37) = 0.63·b.
То есть, постоянная времени T системы первого порядка равна отрезку времени, за которое переходная функция достигает 63% своей установившейся величины. Отметив на графике 63% установившейся величины переходного процесса, определяем абсциссу этойточки (параметр Т);
г) постоянную Т можно также определить следующим образом. Продифференцируем решение и устремим t к 0, тогда
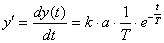 ,
, 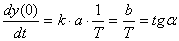
здесь α – угол наклона касательной к графику функции при t = 0.
Тогда 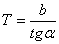 . Итак, величина T - отрезок оси, равный расстоянию от начала координат до точки, в которой касательная пересекается с асимптотой (т.к.
. Итак, величина T - отрезок оси, равный расстоянию от начала координат до точки, в которой касательная пересекается с асимптотой (т.к. 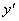 - угловой коэффициент касательной). Это решение самое простое, однако, не самое точное, так как очень трудно провести точно касательную и определить точно ординату асимптоты b.
- угловой коэффициент касательной). Это решение самое простое, однако, не самое точное, так как очень трудно провести точно касательную и определить точно ординату асимптоты b.
Если переходная функция запаздывает на время τ, то есть равна 0 в течение промежутка времени τ после приложения ступенчатого возмущения, то система имеет чисто временное запаздывание, для которого преобразование Лапласа есть e-τs. Следовательно, если переходная функция системы равна
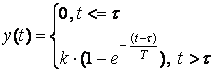
то передаточная функция системы получается в виде 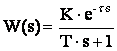 .
.
 2015-02-04
2015-02-04 1486
1486
