Идентификация с помощью частотной характеристики

Частотные характеристики широко используются для анализа и синтеза систем регулирования. Но они также дают возможность определения уравнений объекта. Частотный метод использует амплитудно-частотные характеристики. Идентификация с помощью частотной характеристики основана на применении синусоидальных сигналов или сигналов, аппроксимирующих синусоидальные, частота которых изменяется в рассматриваемом интервале.

Эти методы обладают рядом преимуществ: большой точностью, так как гармонические входные сигналы ортогональны в разных точках измерения и, таким образом, каждая точка частотных характеристик определяется независимо от других; простотой обработки; возможностью проведения измерений в замкнутой системе; малым влиянием шумов.

Недостатки: сложность и большое количество оборудования для проведения измерений на низких частотах; большое время измерения; необходимость преобразования сигналов; условия измерения и параметры исследуемого объекта успевают измениться за время наблюдения.

Как известно, при преобразовании по Фурье отношения входа и выхода, имеем

Y(jω) = W(jω)·X(jω)

где W(jω) – передаточная функция системы при частоте ω. Это комплексная величина

W(jω) = α(ω) + j·β(ω);

│W(jω)│= ;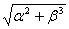

φ(ω) = arg[W(jω)]= .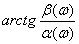

Если на вход объекта подается синусоидальное воздействие A₀sin(ωt) на различных частотах, то установившееся измеренное значение выходного сигнала

y(t) = A₁sin[ωt + φ(ω)] + n(t),

где n(t) - ошибка измерения, 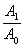=│W(jω)│, φ = Arg[W(jω)].

Частотная характеристика W(jω) определяется путем подачи синусоидальных входных сигналов A₀sin(ωt) на различных частотах ω и записи соответствующих выходных сигналов A₁sin[ωt + φ]. С целью получения необходимой частотной характеристики, величины A₁/A₀ и φ определяются для каждой рассматриваемой частоты ω. То есть по записям входного и выходного сигналов определяют отношение амплитуд на частоте ω_i и получают |W(jω_i)|. Фазовый сдвиг φ(ω_i) получают из сравнения положения максимумов кривых x(t) и y(t).

Рассмотрим на примере процедуру идентификации объекта, в частности, определение передаточной функции на основе экспериментальных частотных характеристик. В результате проведенных экспериментов, измерив входные и выходные сигналы, а затем определив, как описано выше амплитудные А(ω) и фазовые φ(ω) характеристики объекта, можем записать

P(ω_i) = A(ω_i)·cosφ(ω_i), Q(ω_i) = A(ω_i)·sinφ(ω_i)

для каждой рассматриваемой частоты.

Напомним, что структурные параметры модели (в данном случае порядок уравнения) определяются на стадии структурной идентификации. Задаемся некоторым (предполагаемым) порядком уравнения. Для определенности предположим, что объект третьего порядка. Тогда

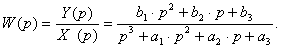(13.6)

Необходимо определить коэффициенты передаточной функции a_i, b_j. Заменим p на jω и запишем передаточную функцию в виде суммы действительной и мнимой частей

.

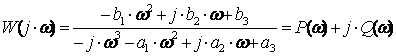Отсюда

.

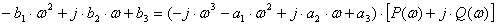Приравнивая коэффициенты при мнимых и действительных частях этих комплексных выражений, получим:

.

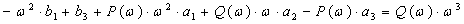
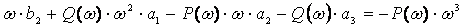Эти уравнения справедливы для всех значений ω.

Подставляя в эти уравнения различные значения частот ω_i и соответствующие им P(ω_i), Q(ω_i), получим систему алгебраических уравнений для определения неизвестных коэффициентов передаточной функции. Так как в экспериментальных измерениях, а следовательно, и в функциях P(ω_i), Q(ω_i), вычисленных на основе этих измерений, имеются ошибки, то вычисленные коэффициенты отличаются от действительных. Для уточнения значений коэффициентов, вычисления повторяются для других частот, и берется среднее из двух вычислений.

Если порядок объекта выше предполагаемого, то в повторных вычислениях значения коэффициентов будут сильно отличаться от первых. То есть сильная разница коэффициентов указывает на то, что порядок объекта занижен (но не указывает на ошибку эксперимента).

При применении полигармонических входных сигналов возрастает помехоустойчивость. Так как спектр частот входного сигнала известен, по измеренным значениям входного и выходного сигналов могут быть получены коэффициенты Фурье для всех интересующих гармоник.