Динамические детерминированные модели

В одномерном случае связь между входной величиной x =x(t) и выходом y = y(t) представляет собой обыкновенное дифференциальное уравнение:

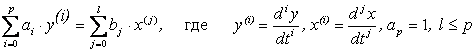, (14.5)

вместе с начальными условиями для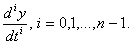

Модель определяется (p+l+1) параметрами c = (a₀,…,a_p-1,b₀,…,b_l).

Для описания динамики объектов, которые характеризуются дискретными значениями входных и выходных сигналов, вместо дифференциальных уравнений можно воспользоваться разностными уравнениями. Обозначив дискретные значения входного и выходного сигналов соответственно x_k-j =x[(k-j)] и y_k-j = y[(k-j)], разностное уравнение (аналог дифференциального) запишем в виде

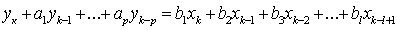(14.6)

Необходимо также задать начальные условия. Структурными параметрами модели являются p и l, которые должны быть выбраны в процессе структурной идентификации.

Модель (14.5) часто удобно записывать в виде системы дифференциальных уравнений. Обозначимy₁ = y, y₂ = y⁽¹⁾, y₃ = y⁽²⁾,…, y_k = y^(k-l). Тогда (14.5) в виде системы имеет вид:

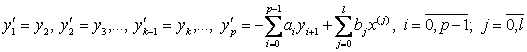(14.7)

(14.5) сводится к (14.7), но (14.7) в общем случае не сводится к (14.5).

Можно записать в обобщенной форме

Тогда векторная форма системы: ,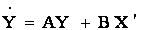

где Y = (y₁,…, y_p) – вектор состояний, X’=(x, x⁽¹⁾, …, x^(l)) – вектор возмущений, A – квадратная матрица коэффициентов, B – прямоугольная матрица коэффициентов.

Итак, исходной информацией для построения процедуры идентификации является вид идентифицируемой модели (14.5) и наблюдения {X_t, Y_t} в промежутке [0,T]. Надо определить a_i, b_j. В общем случае при подстановке наблюдений в уравнение модели (14.5) равенство в этом уравнении не выполняется. Надо подобрать a_i, b_j таким образом, чтобы в уравнении (14.5) правая и левая части отличались друг от друга наименьшим образом.

Строим функцию невязки в виде среднего квадрата разности правой и левой части уравнения (14.5) при подстановке туда функций X_t, Y_t – наблюдений объекта

. (14.8)

Минимизируем (14.8) по a_i и b_j: 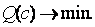Результат минимизации – с* дает значения идентифицируемых параметров. c*=(a₀*,…,a_p-1*, b₀*,…,b_l*) – решение.

Приравнивая нулю производные функции (14.8) по всем неизвестным параметрам (так как функция гладкая), получим систему линейных уравнений, решение которойявляется решением задачи минимизации.

Полученную систему можно решить стандартными вычислительными методами. Однако для вычисления коэффициентов системы необходимо знать производные входного x_t и выходного y_t сигналов объекта. Если эти сигналы заданы в аналитической форме – нет никаких проблем. В противном случае надо выбрать метод получения производных; это зависит от конкретных условий и должен определяться каждый раз специально:

1) можно использовать численное дифференцирование, то есть использовать точечную оценку производных:

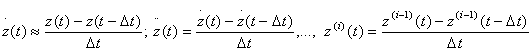(14.9)

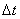- интервал, характеризующий базу оценок. Этот метод обладает двумя недостатками. Во-первых, точность оценки производных быстро падает с ростом порядка производных. Практически хорошо оценить производные выше второго порядка не удается. Во-вторых, для оценки i-той производной при t=0 необходимо иметь значения функции приt<0, то есть z(-∆t),z(-2∆t), …, z(-i*∆t). Так как этих значений нет в измерениях, то приходится в (14.8) брать пределы интегрирования не [0,T], а [i*∆t, T], где i – номер максимальной производной функции;

2) можно использовать аппарат сглаживания функции с весом ρ(t); либо

3) разложение в ряд по заданной системе функций (из-за наличия операции сглаживания, ошибки в определении производных будут значительно меньше).

Для того чтобы задача идентификации имела решение, необходимо, чтобы определитель системы, полученный в результате решения задачи минимизации, был отличен от 0. Если это условие не выполняется, то следует взять другую реализацию входов и выходов объекта, либо уменьшить количество идентифицируемых параметров (то есть p иl), то есть уменьшить порядок модели. Первая мера не всегда приводит к цели, а вторая – при последовательном применении – всегда.