Существуют два основных метода интегрирования: подстановка и «по частям».
Введение новой переменной в неопределенном интеграле производится двумя способами:
1) если 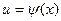 , где
, где 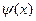 - дифференцируемая функция, то
- дифференцируемая функция, то
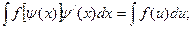
2) если 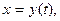 где
где 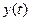 - монотонная, дифференцируемая функция новой переменной t, то
- монотонная, дифференцируемая функция новой переменной t, то 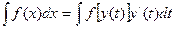 .
.
Примеры.
1. 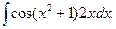
Полагаем, 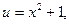 находим
находим 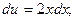 получим:
получим:
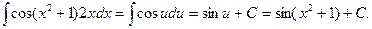
2. 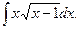
Полагаем, 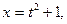
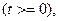 отсюда
отсюда 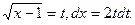
Следовательно,
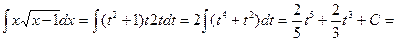
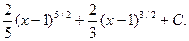
Найти интегралы:
23. 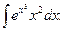
24. 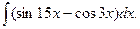
25. 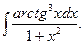
26. 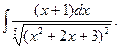
27. 
Если подынтегральное выражение можно представить в виде дроби, в числителе которой стоит дифференциал знаменателя, т.е. дроби вида: 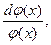 то интеграл можно вычислить по формуле:
то интеграл можно вычислить по формуле:
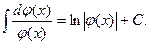
Примеры.
1. 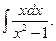
Найдем дифференциал знаменателя: 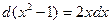 ; сравним полученный результат с числителем. Очевидно, что числитель надо помножить на 2; чтобы дробь не изменилась, помножим на 2 и знаменатель, получим:
; сравним полученный результат с числителем. Очевидно, что числитель надо помножить на 2; чтобы дробь не изменилась, помножим на 2 и знаменатель, получим:
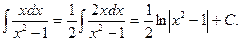
2. 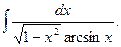
Найдем 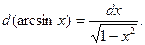 В числителе стоит дифференциал знаменателя, поэтому получим:
В числителе стоит дифференциал знаменателя, поэтому получим:
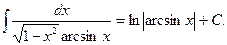
Рекомендация. Если подынтегральная функция – дробь, то надо проверить, не является ли числитель дифференциалом знаменателя.
Найти интегралы:
28. 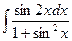 ,
,
29. 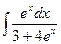 ,
,
30. 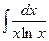 ,
,
31. 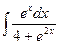 ,
,
32. 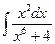 ,
,
33. 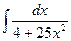 ,
,
34. 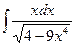 ,
,
35. 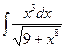 .
.
В заданиях 31-35 после выполнения соответствующей замены в знаменателе появляется выражение вида 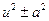 , содержащее полный квадрат. Это делает возможным применение одной из формул VIII, IX, XII, XIII.
, содержащее полный квадрат. Это делает возможным применение одной из формул VIII, IX, XII, XIII.
В случае, если знаменатель содержит квадратный трехчлен общего вида 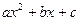 следует сначала выделить полный квадрат. Напомним, как это делается.
следует сначала выделить полный квадрат. Напомним, как это делается.
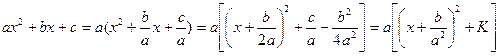 ,
,
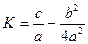 .
.
Примеры
1. 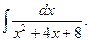
Выделим из квадратного трехчлена полный квадрат:
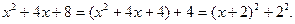
Полагая 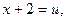 получим:
получим:
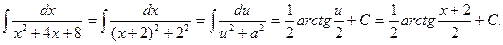
(Применили табличный интеграл IX).
2. 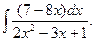
Так как подынтегральное выражение – дробь, то проверим, не является ли числитель дифференциалом знаменателя. Найдем
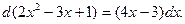
Чтобы выделить это выражение в числителе, выполним следующие преобразования:
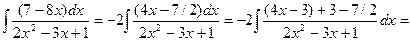
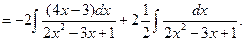
Заметим, что первый интеграл – табличный (III); для второго преобразуем знаменатель:
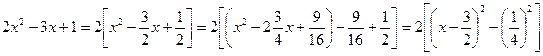 ;
;
затем, полагая 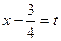 , найдем dx=dt и подставим в интеграл:
, найдем dx=dt и подставим в интеграл:
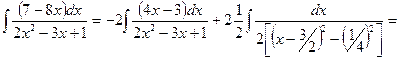
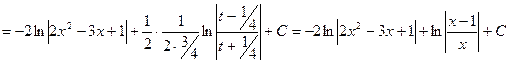 .
.
(Применяя табличный интеграл XII).
3. 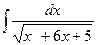 .
.
Преобразуем подкоренное выражение:
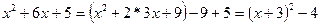
и, полагая х+3=u, dx=du, получим:
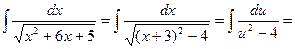
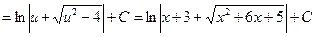 .
.
(Применена формула XIII).
4. 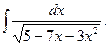
Преобразуем подкоренное выражение:
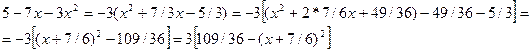
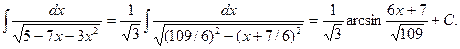
Найти интегралы:
36. 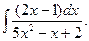
37. 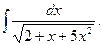
38. 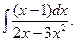
39. 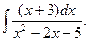
40. 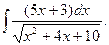
Вопросы и задания для самоконтроля.
1. Докажите формулы: XIV. 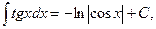
XV. 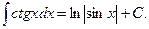
2. В чем отличие формул VIII и XIII таблицы интегралов?
3. Проведите вычисление интегралов в общем виде:
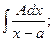
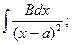
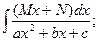
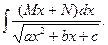
4. Объясните, почему в методе подстановки требуют, чтобы функция
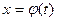 была монотонной и дифференцируемой?
была монотонной и дифференцируемой?
5. Найдите интегралы (если нет затруднений, можно устно):
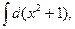
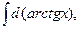
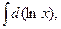
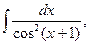
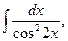
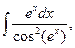
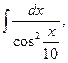
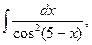
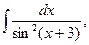
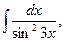
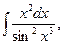
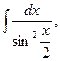
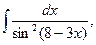
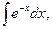
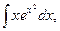
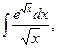
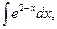
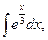
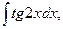
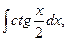
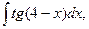
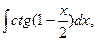
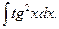
 2015-02-04
2015-02-04 2123
2123








